[Nengo Loihi]: Computable functions and Spiking Behaviour

Deep Learning
1

Hello everyone,

I had few questions with respect to Nengo Loihi mentioned below.

Q1. Let’s say I have a converted TF trained network with nengo.SpikingRectifiedLinear() neurons. As we know, nengo.SpikingRectifiedLinear() can output multiple spikes in a time-step during simulation. Is outputting multiple spikes by a neuron in a single time-step supported on Loihi chips (or by Nengo-Loihi)? From the code here output[:] = spikes_mask * (self.amplitude / dt), it seems that it supports only a single spike by each neuron in a single time-step. Please clarify.

Q2. What type of functions can we compute with Nengo-Loihi? A square/product function can be computed with Nengo, what about its computation with Nengo-Loihi (and with which Loihi neurons)? Is any function computable with spiking neurons in Nengo also computable with Nengo-Loihi on Loihi chips or just the linear functions are computable on Loihi?

Q3. Further, I know that any Nengo object (obtained after conversion of TF trained model) can run on Loihi, whereas rest TensorNodes have to be run off-chip (i.e. on GPU/CPU); hence, wanted to know what should be the properties of a function to be embodied in a Nengo object.

Please clarify. Thanks!

2

No. If memory serves me correctly, the neuron code defined in NengoLoihi’s neurons.py file basically emulate the behaviour of the neurons implemented on the physical Loihi chip. What this means is that the neurons in both NengoLoihi and the physical Loihi chip can only spike once per timestep.

The beauty of the NEF formulation is that, given enough neurons, you can compute even non-linear functions with any type of neuron. All you need to know is the neuron response curves given a range of inputs. Even without this fact, the neurons implemented on the Loihi chip are essentially LIF neurons, and so you’d be able to “compute” any function that is “computable” by regular LIF neurons. Note that I put “compute” in quotes because the neurons aren’t actually computing the function, rather, they are approximating the function for a specific range of input values.

I’d have to get the full list from the devs, but just taking a quite look at the code it looks like the Dense and Convolution layers are fully supported. Basically, anything that can be converted to Nengo objects (ensembles and passthrough nodes) will be converted to on-chip equivalents.

3

Thank you @xchoo for looking into this. With respect to Q1, I am clear.

When you mention regular LIF neurons in th following:

you mean the nengo.LIF() neuron types… right?

About Q3, I wanted to know the properties of general functions which are computable on Nengo-Loihi (or for that matter… on any neurmorphic chip). Sorry for the confusion/vagueness here. Following might make it more clear. I can see that in here, you create TensorNode if activation type is not found in this dict (I hope I am following the code well), whereas for others (be it Convolution/AveragePooling) you create Nengo Objects and use the nengo.Convolution() object to bring the Convolution/AveragePooling operation in effect, as can be seen here and here respectively. This makes me think that the transformation matrices that you build (with supposed intention to come up with objects to have on-chip execution) should be linear matrices, i.e. the functions (i.e. AveragePooling, etc.) embodied in Nengo Objects should be linear. Is this the strict property of a function which makes it eligible for on-chip computation (I am wondering if my question even makes sense)? My next question might bring more context. As we know, MaxPooling layers don’t have a Nengo Object equivalent, rather it is a TensorNode after nengo_dl.Converter() operation. Now, MaxPooling is not a linear operation, thus cannot be converted to Nengo object. Is this understanding correct? With respect to this, there’s a subtle lack of my understanding of add_nengo_obj() too. Since MaxPooling doesn’t have activation and activation_map has an entry of None key, how come the creation of a TensorNode for MaxPooling layer is brought into effect in the code flow? I am certainly missing some code aspect here. Please let me know.

4

This is correct.

You are correct in the observation that currently, all of the transformations (convolution, average pooling, etc.) supported by the NengoDL converter are linear transformations. The reason for this is somewhat nuanced, however.

In my previous post, I mentioned that Nengo and NengoLoihi networks can “compute” (approximate) any function, even non-linear functions. The obvious question here is, of course, why only linear transformations are included in the NengoDL converter by default.

Let us examine linear transformations first. Since the transformations are linear, they can be incorporated into the connection weights in a straightforward manner using the appropriate matrix operations. These matrix operations are defined by the linear transformations themselves and have no addition parameters to tweak (since it’s just a matrix multiply), so we know the exact “solution” as to how to integrate such things into the Nengo network. Since we know the exact “solution”, linear transformations can be implemented in the NengoDL converter with too much difficulty, and are included by default.

What about non-linear functions? In Nengo, non-linear functions are “computed” by solving for the appropriate connection weights such that for a given input to a neural ensemble, the weighted activation functions approximate the desired function. Note, however, that in all of our Nengo examples that compute non-linear functions (e.g., product, square, etc.), an ensemble of neurons is required to compute the function. This is where the difficulty lies in incorporating such functionality into an automatic converter. In TF for example, you could apply a max pooling function on the output of a layer, like so:

input --> neurons --> max pooling --> output

But, to do the same thing in Nengo, since the max pooling function is non-linear, you’ll need an additional ensemble of neurons to perform this computation:

input --> neurons --> ensemble --> (weights computing max pooling) --> output

The specific details of this additional ensemble are typically application / user dependent (e.g. what range of values the input has, to what accuracy does the user want the non-linear function approximated, number of neurons to use in this additional ensemble, neuron parameters for this ensemble, etc.), so it becomes impossible to build a “default” converter for these non-linear functions. Instead, we leave it up to the user to extend the NengoDL converter to implement the desired non-linear functions to their own specifications.

Just to summarize, this statement is partially correct, and partially incorrect. As I described above, something like max pooling isn’t natively supported by the NengoDL converter, so in that sense it “cannot be converted to a Nengo object”. However, the function itself can be approximated in a Nengo network, so if the user takes the time to implement their own converter function to do so, something like max pooling can be converted to use only Nengo objects.

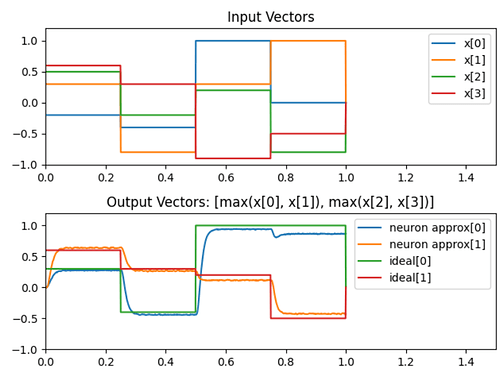
Here’s some code demonstrating the max pooling function being computed using only Nengo objects: test_max_pool.py (1.3 KB)

The max pooling operation is being performed on a 4D vector, where the function computes [max(x0, x1), max(x2, x3)]. And this is what the output graph looks like:

image
image793×590 73.4 KB

Note: I made the ensemble with 1000 neurons because I didn’t want to fuss around with optimizing it. I just knew that 1000 neurons would have been more than plenty to approximate this function. Even 200-ish will work, but you can test that on you own.

Note 2: There are also other tricks you can use to optimize the neural implementation of the max pooling operation. As an example, instead of having 1 ensemble to the full 4D input, I could have used an EnsembleArray (source docs here) and split the input into 2 sub-ensembles before doing the max function. This approach scales up better to larger inputs. E.g., if you had a 16x16 matrix and you wanted to do a 2x2 max pooling, instead of a 256D ensemble with something like 25600 neurons (which would take a long time to solve the decoders for), you’ll instead use an EnsembleArray with 128 sub-ensembles, with each sub-ensembles being 4D and maybe 400 neurons (which doesn’t take a long time to solve the decoders). i.e., instead of this:

nengo.Ensemble(25600, 256)

we do this:

nengo.networks.EnsembleArray(400, n_ensembles=128, ens_dimensions=4)
1 Like
5

Thank you for a detailed explanation. Using EnsembleArray seems promising, although I think it might still take some time (say like 5ms to 10ms or so) to compute a reasonable max at every layer (irrespective of the magnitude of . Isn’t it? Also, will the execution of EnsembleArray op to calculate max be parallel for all the 256D inputs?

BTW, I have further more questions with respect to running networks on Nengo-Loihi, pertaining to the architecture of the chip. So, when I convert my TF networks, I see the converted network to be comprised of one or more objects of the following types: Ensembles or Nodes or TensorNodes. All the layers having TF neurons with their spiking counterpart are converted to Ensembles, AveragePooling (which is a linear transform operation) gets converted to Nodes, and MaxPooling (which is non-linear) or unsupported neuron types (e.g. softmax) gets converted to TensorNodes.

Now, the Loihi - 1 chip consists of approximately 130000 spiking neurons (arranged in 128 Neurocores, with each having 1024 neurons) along with 3 CPUs for management. A neuromorphic board can have N numbers of Loihi chips and I am assuming that the board is connected to other computing resources too, e.g. a larger pool of memory, some extra CPUs and GPUs. My question is: where do the respective objects i.e. Ensembles, Nodes, and TensorNodes run? My guess is that Ensembles run on Loihi Neurocores as they require spiking neurons, and Nodes and TensorNodes run on either (Loihi) CPUs or GPUs (TensorNodes most likely runs on GPUs as they execute TF codes).

With respect to the power savings, execution of Ensembles on Neurocores proves to be highly beneficial (right?), whereas my (assumed) execution of Nodes and TensorNodes on CPUs/GPUs might even result in higher power consumption (than normal TF execution on GPUs due to their execution for each time-step), so possibly no power savings for such a network comprised of non-Ensemble objects. Am I right here?

My other direct questions (which are related to above questions) - where does the Node run? Off-Chip or On-Chip CPUs? Is the particular action of Linear Transform (through nengo.Convolution) executed on CPUs/GPUs and then the resultant values are passed to Neurocores (to receive spiking output) in case of TF Conv operation? Do only those operations which require spiking neurons (e.g. the EnsembleArray method to compute max) executed on Loihi (i.e. its CPUs are not used, rather only the Neurocores for computation)?

What I have learned from posted Nengo-Loihi tutorials is that first and last layers are generally executed off-chip to generate spikes and collect predicted outputs. I am fine with it, my main concern is the execution of intermediate layers. I may be wrong in my above assumptions, hence please let me know if my questions don’t make sense. I will probably do some more research on the Loihi architecture before I get back (and will appreciate if you could link me to some of them in light of my above questions)!

6

That is correct. Because you need an ensemble (or ensemble array) to compute the max pooling operation, it incurs a 1 connection delay compared to the TensorNode implementation. The actual delay will depend on the synaptic time constant you use in the connection. The delay time (for the nengo.Lowpass synapse) is about 2/3 * synapse.tau.

Yes, generally. The EnsembleArray consists of a number of ensembles in parallel, so they should all be computed in the parallel.

The nengo.Ensembles do run on the Loihi neurocores, yes. As for nengo.Nodes, it depends on what kind of node it is. For passthrough nengo.Nodes (nodes that have no function – other than the identity function – applied to the output), they are actually removed from the Nengo network before it is put on the Loihi chip. For non-passthrough nengo.Nodes (nodes that generate an output, or apply a function to an input signal), they are run on the host system (i.e., your PC). I haven’t tried running TensorNodes with NengoLoihi, but I know it will be run on your PC. I’ll have to check with the devs as to whether it runs on the GPU or CPU though (I would guess GPU though)

In general, yes, but the answer is more nuanced. You’ll only get the power savings (by using spikes) if you run your network on the Loihi board. For networks that process data in real time (i.e., batch size = 1), you will observe this happen. However, for networks that can process batch data, you’ll observe that you get more power savings (per inference) if you run it on the GPU, but only because you can process more batches per unit time than you can on the Loihi board.

Non-passthrough nengo.Nodes will run off-chip (on your PC).

Becuase the Conv operation is linear, the nodes created by the NengoDL converter should be counted as passthrough node, and should be removed from the network before it is put on the Loihi board.

Yeah, if you use NengoLoihi, all of the nengo.Ensembles, regardless of where they are in the network, will be run on the Loihi board. Because of this, you need to be careful how the network is structured. If you do something like this:

input --> Ensemble A --> non-passthrough node --> Ensemble B

you get off-chip then on-chip communication between ensemble A and B, which makes the network run slower than if everything was on the board.

Yeah, in my example above, the information flow would look something like this:

input (PC) --> on-chip neurons --> Ensemble A (on-chip) --> off-chip neurons --> non-passthrough node (PC) --> on-chip neurons --> Ensemble B (on-chip)
7

Hello @xchoo!

Thank you for the above information along with others. I am bit confused about the following:

TF Conv layers can be configured with neurons e.g. ReLU. And TF AveragePool layers just have a linear transform equivalent in Nengo as nengo.Convolution(). As the AveragePool layers are represented as nengo.Node(), I am coming to a “loose” conclusion that TF Conv layers with ReLU neurons are subdivided as two separate operations, 1st: a nengo.Node() object to convolve learned filters (during inference phase), and 2nd: a nengo.Ensemble() equivalent object which has spiking neurons to output on the convolved input (from the nengo.Node() of the TF Conv layer).

You mentioned that Conv operations are linear (which indeed it is in the absence of following ReLU neurons - please note that I am combining ReLU neurons with convolution operation as a TF Conv op and they need not be combined). My first question: the linear transform operation on the input is a non-identity operation, hence shouldn’t it be considered as a non-passthrough node as the linear transform operates on the input and produces a new output? My second question (relates to first): If the linear transform (i.e. nengo.Convolution()) is a non-passthrough Node op (assuming I am correct in my first question), then the output is sent to the Loihi neurons from the PC to compute spikes and there will be a communication delay, if yes… what’s the order of this delay? My third question: If at all the nengo.Convolution is a pass-through node, then AveragePooling equivalent nengo.Node() will be a pass-through node and it will be removed from the deployable nengo.Network(). Then where would the linear transform operation take place? It’s not a spiking based operation, it’s just an element wise multiplication followed by sum (in case of AveragePooling or nengo.Convolution() for that matter).

With respect to the following:

I guess one is better off with all the layers being one of nengo.Ensemble() or pass-through nengo.Node() to leverage the power efficiency of the Loihi chip to the maximum. A small doubt pertaining to my understanding with respect to the following:

the off-chip neurons after the Ensemble A (on-chip) denotes a communication channel to the PC (or host) right? and similarly the on-chip neurons after the non-passthrough node (PC) means a communication channel to Loihi board… isn’t it? And Ensemble A/B (on-chip) denotes the on-chip spiking computation? Please let me know.

8

This is generally correct, yes. Although the convolution filters don’t necessarily have to be learned, you can specify them when you create the TF network.

Oh yes. When I mentioned the convolution operation being linear, I only meant the convolution transform, and was not including any non-linearity you apply to the signal after the convolution transform.

No, because the convolution transform is a linear transform, it can be implemented in the connections weights to and from the conv node. This means that the conv node’s functional output is still the identity function, which means that it is still considered a passthrough node. Any node is a passthrough node if the node’s output function doesn’t alter the input signal (i.e., it’s an identity function). Any transforms applied to the signal before or after the node are part of the nengo.Connection object, and do not impact the node itself.

In Nengo, you have to be kind of careful with this though, because you can implement two functionally identical networks using different components. As an example, the following Nengo network doubles an input signal:

with nengo.Network() as model:
    in_node = nengo.Node(input_func)
    x2_node = nengo.Node(output=lambda t, x: x * 2, size_in=1)
    nengo.Connection(in_node, x2_node)

Alternatively, this Nengo network also doubles an input signal:

with nengo.Network() as model:
    in_node = nengo.Node(input_func)
    x2_node = nengo.Node(size_in=1)
    nengo.Connection(in_node, x2_node, transform=2)

In the first network, you will notice that we specified a custom function as the node’s output function. In this case, this makes the node non-passthrough. In the second network, we didn’t implement a custom output function, but rather implemented the linear transform with the nengo.Connection’s transform parameter. In this case, since the x2_node has no custom output function, it is considered a passthrough node.

That’s correct, these linear transformations are non-spiking, and they would be implemented in the connection weights between the respective neural ensembles.

Yes, in order to maximize the power efficiency of the Loihi chip, you’ll want to minimize the on/off-chip I/O, which in turn means you’ll want to have as much of the network (except for input and output nodes) be nengo.Ensembles. They don’t necessary have to be one giant ensemble though, a lot of ensembles will work as well. I must note that we have encountered issues when the number of ensembles was too big, and the network spanned multiple chips. In this case, we were bottlenecked by the interchip communication protocol, but the last I heard, Intel was working on this problem.

Both the off-chip neurons and on-chip neurons are run on the Loihi board. But they are special Nengo created spiking ensembles that have been custom tuned to perform I/O operations. The non-passthrough node (PC) is the part that would run on your PC, and the on/off-chip neurons forms the bridge between the PC and the Loihi network.

Yes, Ensemble A/B (on-chip) are the ensembles that run on the Loihi neurocores and do the spiking computation.

9

Hello @xchoo, the example networks were very helpful to understand the nuances.

This above resolves my doubt of the node type of AveragePooling op; it’s a passthrough node as the weights are applied on the connections between ensembles. When obtaining the node objects after conversion, is there any attribute which can tell whether the node is a passthrough or not. One can obviously check the type of computation done by the node to determine its type, but programmatically determining it would be handy.

About the specifics of the multiplication of weights and their subsequent addition… where is this op (effectively the nengo.Connection() operation) done? On Loihi Board CPUs? or host PC?

With respect to following:

I guess I can safely add the nengo.EnsemblesArray object too to the list of nengo.Ensembles and passthrough nengo.Node for the complete execution of network on Loihi board (except the input and output layer). Right? Also, I am bit confused by off-chip neurons and on-chip neurons now. You mention that:

so, what’s the difference between on-chip neurons and off-chip neurons when both

I guess… they are different in the ways of handling the incoming data with respect to the data’s immediately next destination. The off-chip neurons deal with the incoming data which has to be computed next on PC and on-chip neurons deal with the data which will be used in the computations done next on the neurocores. Is it?

In addition to above questions, can we be certain that all non-passthrough nodes would execute on PC and will consume less I/O (or communication) time than TensorNodes executed on GPUs?

10

Yes! You can check if the nengo.Node’s output is None. This should apply to both regular Nengo nodes (created in a Nengo network) or in a converted TF network.

def is_passthrough(node):
    return node.output is None

Matrix operations are done on the Loihi board.

I’m glossing over a lot of detail here, but generally, the on-chip neurons are specially tuned neurons that read a real-valued signal and convert it to a spike train. All of the communication and computation done on the Loihi board are done with spikes, so the on-chip neurons are needed to convert any real-valued input signal into a spike train.

The off-chip neurons do the opposite. They take the spike trains and convert them back into real-valued signals by applying a custom synaptic filter on the spike train.

No. Comparing Loihi performance to GPU performance is application and network dependent, so there’s no hard and fast rule to apply here. You’d need to test this for yourself unfortunately. Generally though, it has been observed that for Loihi networks, the chip-to-PC I/O (regardless of whether stuff is run on the CPU or GPU) is the largest bottleneck when it comes to simulation speed, so reducing the amount of data being sent to/from the chip will have a good impact on the speed of your simulation.

11

With respect to above, I am understanding that AveragePooling op is done on Loihi Board, and by Loihi Board you mean specifically the CPUs on it. Right? Two questions: as far as I know in limited knowledge, the Loihi Board is a collection of multiple Loihi Chips (let’s say 768 for Poihiki Springs board) and each chip has 3 “x86” Lakemont CPUs, so is the computation of AveragePooling done on all the 768 x 3 CPUs in parallel, or are there some other extra compute CPUs on Loihi board to execute AveragePooling? Irrespective of the computation platform/resource, will not executing AveragePooling on GPUs be more efficient (with respect to computation time as well as power wise too perhaps - since the execution of AveragePooling is not on spiking neurocores)?

In a Nengo model, three important (and repetitive) ops are: Convolution (or any linear transform which includes matrix multiplication and summation of weighted inputs), Spike generation, and Synaptic filtering, apart from the Input and Output of course. From the discussion so far, I have learned that Convolution is done on Loihi Board (i.e. CPUs on it perhaps) and Spike generation is done on neurocores, where is the Synaptic filtering operation executed? again on Loihi Board CPUs? Apart from the above three ops, are there any other major op which I am missing and where are they executed? For Nengo-DL though we can have few pieces of code (which are in TensorNode) which execute on GPUs.

I am bit confused about the implications of the above statement. When you say computation done on the Loihi board are done with spikes as well as

are you implying that matrix multiplication operation and addition are done via spikes?

With respect to the following

I guess, the conversion is done every time-step, so a scalar is converted to an instantaneous current value, followed by its injection to the neuron which can result in it producing a spike if its voltage crosses the threshold. Right? I don’t want to get into the specifics, as I understand that there’s a lot of details here… just trying to understand the operation of on-chip neurons overall.

12

No. The architecture of the Loihi board is not the same as a traditional CPU, so I hesitate to use the word “CPU” to describe it. By “Loihi board”, I mean a collection of Loihi chips. In each chip, there are several neurocores, which contain circuitry to do the neuron activation function computation, as well as any connection weights (matrix operations) necessary. Each chip also contains a few lakemont CPUs, which are in charge of handling I/O and timing signals. If you want to know more about the architecture of the Loihi chip & Loihi board, I recommend posting on the INRC forums.

If you consider just execution time, it will be more “efficient” to perform the AveragePooling operation on a GPU, yes. However, if you are considering power, then no, it will probably still be more efficient to perform the AveragePooling on the Loihi chip. This is assuming a batch size of 1 though. For larger batch sizes, the GPU gets more efficient if you amortize the power across the size of the batch.

We discuss the relationship between energy use and batch sizes in this paper (although, you should note that this is for one specific application, so it may not necessary generalize to others).

If I recall correctly, the matrix multiplication operations are done on a per spike basis within the Loihi neurocores, but I’ll have to double check that.

Essentially, yes. The on-chip neurons is just a specially tuned nengo.Ensemble, but it functions the same as regular ensembles.

13

Sorry for being a bit persistent here… but with respect to the following,

does it mean that the AveragePooling op is done by neurocores without the generation of spikes of course?

I guess the above relates to the question I have asked. Please let me know accordingly and also what per spike basis means.

And thanks for the paper… that should definitely give me some context about the energy usage and related :slight_smile: .

14

That is correct. The average pooling operation can be performed purely in the connection weights, and does not require any additional neural ensembles (i.e., no additional spike generation) to do it.
For example, if you had an ensemble A with 4 neurons and an ensemble B with 2 neurons, and you wanted to compute a (2x1) average pooling, the connection weights between the two ensembles would look like this:

image
image891×750 36.4 KB

You’ll notice that no additional ensembles are needed between ensemble A and B to compute the average pooling operation.

In the Loihi board / chip, whenever a neuron spikes, a “network” packet is generated and sent from the neurocore simulating the source neuron to the neurocore simulating the destination neuron. When the packet arrives at the destination neuron, several computations are made, one of which is the connection weights computation. Since the connection weights serve to connect individual neurons, there is only 1 connection weight between 2 neurons. Since there is only 1 connection weight between 2 neurons, this only needs to be computed if a spike is transmitted from the 2 neurons involved with that connection weight. Thus, the connection weight matrix operations are only computed on a per spike basis.

15

Hello @xchoo, thanks for resolving the doubt about the computational substrate for the AveragePooling op. This execution of the sum of weighted inputs in neurocores holds true for any nengo.Convolution() operation I suppose. Just confirming… in your posted network above, the output from Ensemble A is filtered (i.e. synapsed) output, which is multiplied by 0.5 and then that serves as input x to Ensemble B where the current J is calculated, followed by the voltage update in Ensemble B’s neurons, leading to spike (if the voltage reaches threshold) and the spike is then further synapsed before outputting from Ensemble B; and thus the AveragePooling op continues if it exists after the Ensemble B layer. Right?

Also, with respect to my previous comment on this thread, I guess following was missed.

In the above question, now one doubt stands resolved, i.e. the Convolution operations are performed on neurocores (of course on Loihi Board). What about Synaptic filtering?

Also, let’s say, I have to calculate inter-spike interval, this can be done in nengo.Node() perhaps as it is supposed to hold any arbitrary python code. The nengo.Node() will then output the inter-spike interval of the selected neurons, therefore I guess… it will be considered as a non-passthrough node, hence executed on host PC… right? If considered a non-passthrough node, is there a way to make it passthrough… I strongly anticipate there should be a way, as spikes are inherent to Loihi Board and calculating inter-spike intervals at each time-step should be trivial (perhaps even a Loihi API exposed for it?). One more question, can we change the weights of the matrices/kernels in nengo.Convolution() every time-step? Sorry for asking these many questions on this thread… :grin:

16

Yes. Although, the synapse filtering computation is done on the input to a neuron, not as an output from a neuron (the output of a neuron is just a spike).

If I recall correctly, the synaptic filtering is performed as part of the connection weight computation on the destination neuron’s neurocore (or just before the neurocore… i can’t remember what intel denotes to be part of / outside the neurocore – regardless, it’s still on the Loihi chip).

That is correct. If you are performing custom python computations in a nengo.Node, that will be performed on the PC.

I don’t believe there is currently a method by which you can measure the firing rates of neurons on the board itself as this requires measurement hardware to be implemented on the Loihi chip itself, which I don’t think is present. However, what you could do is use the NengoLoihi’s Loihi “emulation” mode to compute the interspike intervals (ISI) on your PC (the emulator runs entirely on the PC, but the firing rates of the neurons should be identical to running it on the Loihi board). Then, to run it on the board, simply disable your ISI nengo.Node.
To use the NengoLoihi emulation mode, do

with nengo_loihi.Simulator(target="sim") as sim:

instead of

with nengo_loihi.Simulator(target="loihi") as sim:

Yes, but if you want to do this, you’ll need to use an online learning rule (probably a custom one?) to achieve this. The online learning mechanisms are the only things on the Loihi board that are able to change connection weights as the simulation is progressing. They do come at a performance cost though, and I’ll have to check with the NengoLoihi devs, as there are some restrictions you need to adhere to regarding online learning rules. Otherwise, you’ll run into the issue where parts of the rule are run on your PC, and parts of it on the Loihi board.

17

With respect to the following:

Actually I need to calculate ISI during inference phase in Nengo-DL (with possible option of deploying the network on Loihi Board), hence was looking for a direct way to calculate it. The IS Intervals would obviously change based on the input, and BTW… I don’t need ISI during training phase or so. Next, I wanted to modify the nengo.Convolution() kernels during inference phase as well. I guess, since this would involve modifying the layers of the converted network in Nengo-DL, I should better open another topic focused on it. Anyways, please do let me know your thoughts about calculating ISI during inference phase with focus on on-board computation (if there exists any way).

18

I spoke to the NengoLoihi devs, and gave it some more thought. If you are just wanting to compute the ISI of neurons in your network, then all you need to do is either probe the neurons (nengo.Probe(ens, "neurons")), or connect to the .neurons object to a Node to compute the ISI. It is true that the node will run on your PC, but as long as you don’t need to feed the output of that ISI node back into the network, it should not slow down your network simulation too much.

The issue with off-chip Node computation is really when you have the output of the node feed back into the network. Then you incur I/O penalties going off-chip (which you already do if you are probing outputs from your network), and additional penalties for feeding the value back to the chip.

This is what the NengoLoihi dev sent me, for context:

Yes, you can probe the .neurons attribute of an ensemble just like you can in Nengo core to get the output spike trains. You can then calculate rate or ISI or whatever.

Note that when precompute=True , we use NxSDK’s spike probes, which are faster but have limits on the number you can have (the limits are per-chip, I think, something like 2048 per chip). With precompute=False , we probe them manually within a custom SNIP, which is a bit slower but it doesn’t have the same limits (though there are still some limits based on the amount of memory available to the SNIP).

19

Hello @xchoo, thanks for giving it second thoughts. Below is a custom script I wrote for the calculation of ISI (haven’t implemented the exact function yet, but it should be straightforward, given that I am able to access the spikes (with amplitude 1/dt) in my _get_isi()). My goal is to calculate ISI for more than 1 input scalar (i.e. more than one inp_node1).

SEED = 89
x1, x2 = 0.9, 0.1

def _get_isi(t, x):
  print(x)
  #return x[0], x[1]
  
with nengo.Network(seed=SEED) as net:
  # Create Input Nodes.
  inp_node1 = nengo.Node(x1)
  inp_node2 = nengo.Node(x2)
  
  # Create 2 Ensembles.
  ens1 = nengo.Ensemble(n_neurons=1, dimensions=1, seed=SEED, radius=1)
  ens2 = nengo.Ensemble(n_neurons=1, dimensions=1, seed=SEED, radius=1)
  
  # Create the ISI Node.
  isi_node = nengo.Node(output=_get_isi, size_in=1)
  
  # Connect the Input nodes to the Input ensembles.
  nengo.Connection(inp_node1, ens1, synapse=None) # Default Synapse is Lowpass(0.005)
  nengo.Connection(inp_node2, ens2, synapse=None) # Default Synapse is Lowpass(0.005)
  
  # Connect the Input ensembles to the ISI node.
  nengo.Connection(ens1.neurons, isi_node, synapse=None)
  nengo.Connection(ens2.neurons, isi_node, synapse=None)
  
  # Check the representation of inputs.
  probe1 = nengo.Probe(ens1, synapse=nengo.Lowpass(0.005))
  probe2 = nengo.Probe(ens2, synapse=nengo.Lowpass(0.005))

  # Check the spiking pattern.
  spikes1 = nengo.Probe(ens1.neurons) # Default synpase is None
  spikes2 = nengo.Probe(ens2.neurons) # Default synpase is None
  
with nengo.Simulator(net) as sim:  
  sim.run(1)
  vctr_points_1, activities1 = tuning_curves(ens1, sim)
  vctr_points_2, activities2 = tuning_curves(ens2, sim)

It runs error free when size_in=1 i.e. when I access spikes for only one input (although there are two connections made to the isi_node:

# Connect the Input ensembles to the ISI node.
nengo.Connection(ens1.neurons, isi_node, synapse=None)
nengo.Connection(ens2.neurons, isi_node, synapse=None)

which I thought… it should throw an error due to size_in=1, but no… no error is thrown. However, when I set size_in=2 to access the spikes for both inputs (i.e. inp_node1 and inp_node2) in function _get_isi(), it throws this error: ValidationError: Connection.transform: Transform output size (1) not equal to connection output size (2). I looked through few scant examples of creating and using Node with size_in=2 (or more), and found that one needs to mention a transform=np.eye(2) in the nengo.Connection() while creating a connection between the ensemble and the isi_node, but that gave me an expression of creating a multi-dimensional ensemble - which I guess is not useful for me, as I want to record ISI from each individual neuron (as done in Nengo-DL, e.g. the vector input is presented to the first Conv/Dense layer for n_steps and each neuron in the Ensemble represents one scalar element of the vector input). Can you please help me with recording the ISI from individual neurons, each representing a scalar?

I have few more questions though, which are sort of related to my question here. In the following tuning curve plots:

plt.plot(vctr_points_1, activities1)

vctr_points_2_tc

plt.plot(vctr_points_2, activities2)

vctr_points_2_tc

you can see that both the neurons have same curve, and that’s because of the same seed value. I see that a scalar of value 0.7 or more will lead both the neurons to spike, and that indeed is the case as can be seen below (filtered output for scalar 0.9):

plt.plot(sim.data[probe1])

do_probe1

However, for scalar input of 0.1, the neuron is not supposed to spike as per the tuning curve plot, and that indeed is reflected below in the filtered output plot.

plt.plot(sim.data[probe2])

do_probe2

Now, since the radius is set to one, I am supposed to input values in range [-1, 1] only, but as can be seen above, it’s not guaranteed that a single neuron will spike for that input (a group of neurons will do). So how is it done in Nengo-DL where one neuron represents each scalar input (either direct input or calculated ones in the network e.g. Convolved ones). Please let me know this too.

20

In Nengo, almost all signals are arrays (Numpy arrays). When you connect to a nengo.Node, the size_in parameter determines the dimensionality of the signal being fed into the node. When you do something like nengo.Node(size_in=2), what Nengo is doing is creating a Node that expects an 2-dimensional array every timestep.

When you connect to / from a .neurons object, Nengo expects / returns an array where the dimensionality is the same as the number of neurons. For every timestep, the value in each dimension of the array denote either the input to that corresponding neuron (connecting to .neurons) or whether or not that neuron has spiked (connecting from .neurons).

That is correct, no error is thrown. This is because you are connecting 1D arrays (the output the .neurons object of an Ensemble with 1 neuron) to the input of the node. Furthermore, by doing this:

# Connect the Input ensembles to the ISI node.
nengo.Connection(ens1.neurons, isi_node, synapse=None)
nengo.Connection(ens2.neurons, isi_node, synapse=None)

what you are actually doing is summing the 1D output of each ensemble together before feeding it to the ISI node. If you set the input x2 to be equal to x1 this will become apparent.

For your specific use case, if you want to connect the .neurons output of different ensembles to the same node, you’ll have to do something like this:

isi_node = nengo.Node(output=_get_isi, size_in=2) # Size in == total number of neurons you want to probe
nengo.Connection(ens1.neurons, isi_node[:ens1.n_neurons], synapse=None)
nengo.Connection(ens2.neurons, isi_node[ens1.n_neurons:], synapse=None)

Here, we use the array slicing feature of connections to connect the output of ens1 to the first ens1.n_neurons dimensions of the isi_node input, and likewise for the neurons output of ens2.

The neurons used in NengoDL networks are typically ReLU or spiking ReLU neurons. Unlike LIF neurons, ReLU neurons have an activation function that is just a ramp, which makes it easier to use 1 single neuron to represent scalar values. For networks that use LIF neurons (and this applies to networks that use ReLU neurons as well), the network training process tunes the connection weights (which affect the gains and biases, and by extension, the intercepts and max_rates, of the neurons as well) such that for the given problem, the neuron representation in that range is most ideal. This is how single neurons are able to represent scalar values for NengoDL / TF trained models (i.e., because they are highly tuned).

In contrast, when you create a random ensemble in Nengo, and connect them to each other using encoders / decoders (i.e., the NEF), the entire ensemble is “generally” tuned (via the decoders) to represent a range of values (default is -1 to 1).