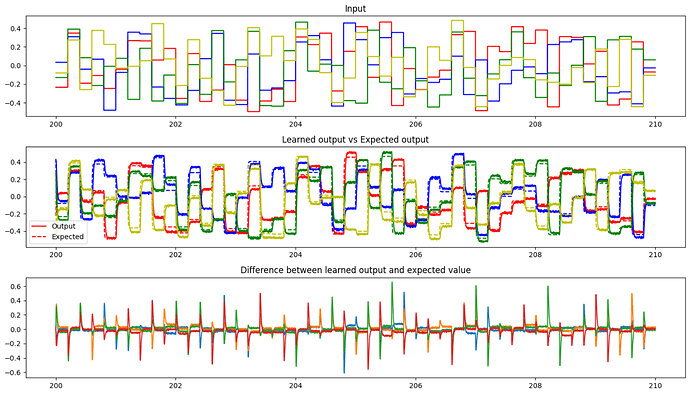
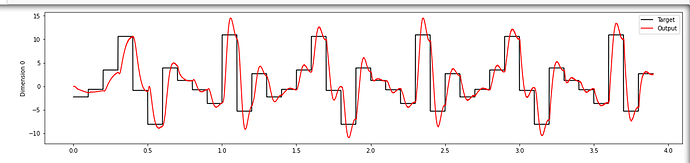
Hi community,
I’m quite new to Nengo and simply trying to comprehend all the examples and also wanted to watch the Summer school videos to become comfortable with the API.
However, as I was experimenting with the examples, I wondered if it was possible to learn a linear transformation in the form of a matrix multiplication (Y = AX) with the PES learning rule.
I thought maybe it could look something like this:
# -- input and pre popluation
inp = nengo.Node([1, 2, 3, 4])
pre = nengo.Ensemble(1,dimensions=4)
nengo.Connection(inp, pre)
matrix = np.matrix([[0, 1, 0, 0], [0, 0, 1, 0], [0, 0, 0, 1], [1, 0, 0, 0]])
# -- post populations
post_pes = nengo.Ensemble(1, dimensions=4)
# -- reference population, containing the actual product
product = nengo.Ensemble(1, dimensions=4)
nengo.Connection(inp, product, transform=matrix, synapse=None)
# -- error populations
error_pes = nengo.Ensemble(1, dimensions=4)
nengo.Connection(post_pes, error_pes)
nengo.Connection(product, error_pes, transform=-1)