Learning a Linear Transformation

[xchoo]

Hi @SebVol, and welcome to the Nengo forums!

@SebVol

However, as I was experimenting with the examples, I wondered if it was possible to learn a linear transformation in the form of a matrix multiplication (Y = AX) with the PES learning rule.

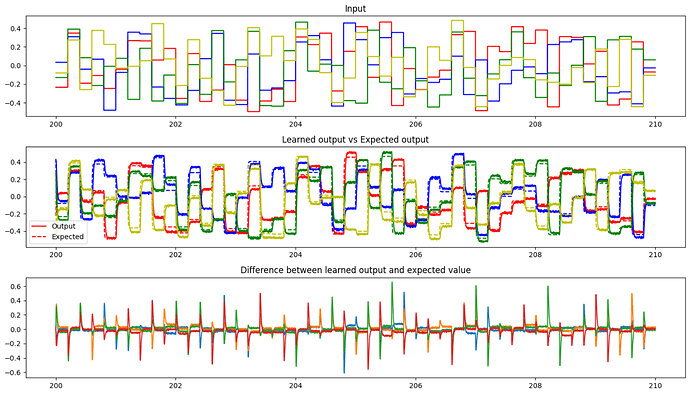
Yes, absolutely! The PES learning rule is quite capable of learning linear (and non-linear) transformations, as evidenced by the examples here. As a bit of a teaser, here’s the output of a network I’ve made that learns a randomly shuffled identity matrix (i.e., it just transposes the order of the vector element around). This output is recorded after the network has been trained for 200s, and while this output is being probed, the learning signal has been inhibited, to demonstrate that the network has generalized the learned connection (similar to what is done in this example).

From the plots, we see that the network has done a pretty good job at learning the shuffled identity matrix.

@SebVol

I thought maybe it could look something like this:

You are generally on the right track, although, there are a few pointers I have for you.

• First, note that in Nengo, by default (if you don’t change the radius value) neural ensembles are optimized to represent values between a certain range. It is typically within the range of a unit hypersphere (i.e., given an vector input, the vector magnitude of said input should be at most 1). While it may be possible for the network to learn with inputs that violate this “constraint” (optimized parameter), for simplicity, you should try to keep the inputs to the ensembles with this in mind.
• As the dimensionality of the ensembles is increased, the number of neurons you use in the ensemble should increase as well. In some networks, we use a scalar multiplier (e.g., 50 * dim), but for the network I put together, I’m using an exponential multiplier (50 * dim ** 1.5). This is mostly from experience, since I know that more neurons will help the network generalize. It does come at the cost of slowing down the simulation, though.
• The network you have proposed should work, with a one minor change (apart from the changes I mentioned above). You seem to be missing the connection between pre and post_pes, which is the one where the learning will actually take place on. Apart from that, the network you proposed should work.