That is correct (i.e., the bias weight does play a role in the firing threshold), but it’s not the full answer. I got into more depth further down this post.
If you are using Nengo, and the nengo.LIF neuron (i.e., the neuron has a range of -1 to 1), and the neuron has a gain of 1, that would be equivalent to an intercept of 0.4. You can test this out with the following code:
import matplotlib.pyplot as plt
import nengo
from nengo.utils.ensemble import response_curves
with nengo.Network() as model:
ens = nengo.Ensemble(1, 1, gain=[1], bias=[0.6])
with nengo.Simulator(model) as sim:
eval_points, activities = response_curves(ens, sim)
plt.figure()
plt.plot(eval_points, activities)
plt.show()
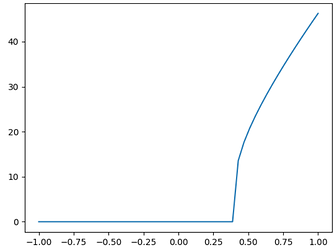
This results in the following response curve:
Note that changing the gain of the neuron will affect the x value at which the neuron starts firing (I assume this point is what you are referring to when you say “spiking threshold”)
To understand why this is the case, we need to look at the LIF equation. In Nengo, the LIF equation is implemented as follows (a(x) is the activity of the neuron for a given input x):
a(x) = \frac{1}{\tau_{ref}-\tau_{RC}\text{ln}(1-\frac{J_{th}}{\alpha x + J_{bias}})}
From the equation, the point at which the neuron starts firing (the x intercept, or x_{int} is when the term inside the natural log goes just a bit above 0 (for values lesser than or equal to 0, this term is undefined). I.e., the neuron starts firing when 1 - \frac{J_{th}}{\alpha x + J_{bias}} > 0. Rearranging the terms, we get:
x_{int} > \frac{J_{th} - J_{bias}}{\alpha}
In Nengo, we use J_{th} = 1 for simplicity, so this equation becomes:
x_{int} > \frac{1 - J_{bias}}{\alpha}
If we substitute a gain value of 1 (i.e., \alpha = 1), and a bias weight of 0.6 (as per your question), we see that the x intercept works out to be 0.4.
What I meant by my statement is that for an LIF neuron on it’s own (no input weight, no bias weight), the spiking threshold is always when the input current just exceeds the firing threshold current (J_{th}). This value is the same for all LIF neurons under the same conditions (no input weight, no bias weight). In Nengo, heterogenous neuron response curves are generated by randomizing the neuron gains and biases.