Spiking threshold as a parameter

General Discussion
2

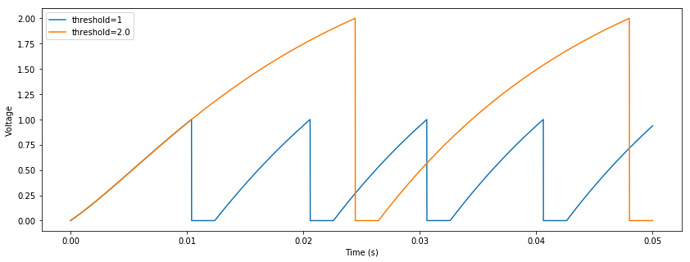
Hi @Vaurien96. Thanks for the question and for taking the time to try to figure out these details and get this code working. I think the most important thing to note is that, for the case of the LIF model, the subthreshold dynamics—what happens to the voltage while it’s operating within the open interval (0, threshold)—are completely linear with respect to the current. Within this operating range, the voltage vector is governed by a leaky integrator (a first-order lowpass filter) – a linear dynamical system applied to the input current.

This observation is important because it tells us that scaling the threshold is mathematically equivalent to inversely scaling the input current by the exact same factor. Another way to say this is that: driving the neuron with an input current of J(t) until it reaches V(t)=1 is the same as driving an identical neuron with an input current R \cdot J(t) until it reaches a threshold of V(t)=R, by linearity. In other words, you can effectively modify the threshold to R (i.e., get the same mathematical outcome) while keeping the actual threshold fixed at 1 by scaling the input current by 1 / R.

Since the input current in the NEF is defined by: $$J = \alpha \left \langle {\bf e}\text{,}\, {\bf x}(t) \right \rangle + \beta$$ and we want to scale J by 1 / R, we can do this by scaling \alpha and \beta by 1 / R, as in: $$\frac{J}{R} = \left( \frac{\alpha}{R} \right) \left \langle {\bf e}\text{,}\, {\bf x}(t) \right \rangle + \left( \frac{\beta}{R} \right) \text{.}$$

In Nengo, \alpha and \beta are referred to as the gain and bias, respectively. These parameters are by default derived from the max_rates and intercepts of the desired tuning curves. This makes the important point that modifying the threshold is mathematically equivalent to modifying your max_rates and intercepts, i.e., your desired tuning curves. These are all completely configurable in Nengo (e.g., see tuning_curves and nef_summary).

Here is some example code that uses this trick to obtain an effective threshold of R = 2, and compares the voltage trace between two otherwise-identical neurons:

import numpy as np
import matplotlib.pyplot as plt

import nengo

threshold = 2.0

with nengo.Network(seed=0) as model1:
    stim1 = nengo.Node(1)
    
    x1 = nengo.Ensemble(n_neurons=1, dimensions=1, encoders=[[1]], max_rates=[100])

    nengo.Connection(stim1, x1)
    p1 = nengo.Probe(x1.neurons, 'voltage')
    
with nengo.Simulator(model1, dt=1e-5) as sim1:
    sim1.run(0.05)
    
gain = sim1.data[x1].gain / threshold
bias = sim1.data[x1].bias / threshold

with nengo.Network(seed=0) as model2:
    stim2 = nengo.Node(1)
    
    x2 = nengo.Ensemble(n_neurons=1, dimensions=1, encoders=[[1]],
                        gain=gain, bias=bias)

    nengo.Connection(stim2, x2)
    p2 = nengo.Probe(x2.neurons, 'voltage')
    
with nengo.Simulator(model2, dt=1e-5) as sim2:
    sim2.run(0.05)
    
plt.figure(figsize=(14, 5))
plt.plot(sim1.trange(), sim1.data[p1],
         label="threshold=1")
plt.plot(sim2.trange(), sim2.data[p2]*threshold,
         label="threshold=%s" % threshold)
plt.xlabel("Time (s)")
plt.ylabel("Voltage")
plt.legend()
plt.show()

threshold_trick
threshold_trick842×320 24 KB

To answer your question a bit more directly, though:

The reason you were seeing this behaviour is because: you not only need to change step_math, but you also need to modify the rates method inherited from LIFRate:

        j = J - 1
        output[:] = 0  # faster than output[j <= 0] = 0
        output[j > 0] = self.amplitude / (
            self.tau_ref + self.tau_rc * np.log1p(1. / j[j > 0]))

The decoding weights are learned from the tuning curves produces by rates, and so these must be consistent with step_math. You can use the observation from above to make the appropriate change by rescaling the input current (J) according to the desired threshold.

To summarize, you can either effectively change the LIF threshold by rescaling the input current, or by using your code and making the rates method consistent with your change. But, in either case, this is mathematically equivalent to rescaling the gain and bias parameters of your tuning curves, which you could also achieve by playing with max_rates and intercepts. If your desired tuning curves remain the same (i.e., if you also updated the gain_bias and max_rates_intercepts methods to be consistent with your new rates method), then this change will have no apparent effect, apart from rescaling the voltage trace.

Please feel free to ask more details about the code, math, or how to use this to do something!

1 Like