Hello everyone!
How can I modeled a 2nd order bandpass filter (post-synaptic current filter) with Laplace transform in nengo? Like this equation:
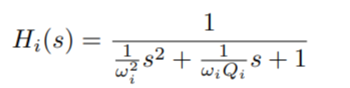
Tranks!
Hello everyone!
How can I modeled a 2nd order bandpass filter (post-synaptic current filter) with Laplace transform in nengo? Like this equation:
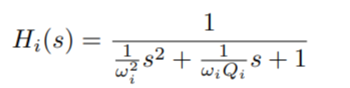
Tranks!
Hi @jone,
This forum thread describes how to implement a high-pass filter in Nengo, and it should be possible to use the same procedure to implement a band-pass filter.
An alternate (possibly simpler) solution is to chain a low-pass and high-pass filter together to get a band pass filter.
Note that the example @xchoo gives is for implementing a bandpass filter as a synapse. If you’re using that as part of a neural model, that would be inherently assuming that the synaptic dynamics are able to implement such a bandpass filter (which may or may not be biologically plausible).
If you’d like to perform this in neurons, you’ll probably want to change it to a state-space system (see scipy.signal.tf2ss for a way to do this numerically). Then, you can apply Principle 3 of the Neural Engineering Framework to determine appropriate input and feedback transform matrices for the input connection and feedback connection on your ensemble, respectively. See here for some general examples of how Principle 3 is applied in practice; your application is actually quite similar to an oscillator (a bandpass filter is a type of damped oscillator).
EDIT: My mistake, the forum thread @xchoo linked does include a neural/NEF implementation. It’s just the end of the thread that then gives a synapse implementation.
Thank you @xchoo and @Eric for the response!
I have implement a bandpass filter as a synapse of the equation, like as follow:
class Bandpass(LinearFilter):
def __init__(self, **kwargs):
hz_w = 250 # Wi - peak frequency
rad_w = hz_w*2*3.14 # Wi - convert peak frequency to rad/s
hz_q = 10 # Qi - bandwidth
rad_q = hz_q*2*3.14 # Qi - convert bandwidth to rad/s
super().__init__([0,0,1], [(1/rad_w**2), (1/rad_w*rad_q), 1], **kwargs)
This is correct?
And other question, can I use this bandpass filter in the nengo.Connection() function (synapse parameter)? Like this:
nengo.Connection(ensamble1, ensamble2, synapse=Bandpass())
Here’s an implementation that’s part of one of our in-progress PRs. You should be able to just copy that implementation into your own code to give it a try, too. It’s slightly different than yours; you can use the example code to plot the frequency response of both of them to compare.
And yes, you can use it in the synapse on a Connection.