We often do something like X*X*X*X (where X is a unitary vector) in order to get some sort of spatial scale in semantic pointers. But, that’s a discrete scale. Can we do something like X**3.5 and get a continuous scale? I’m not quite sure what that would mean mathematically…
4 Likes
Yes, we can! To understand this, it is best to think about this in the Fourier space. When, we do X*Y (* being circular convolution), it is an elementwise product of the complex Fourier coefficients. The product of two complex numbers can be interpreted as a rotation and scaling of one of the numbers by the other number. Now, who says that we have to do the full rotation and scaling? Instead, we could do only “half”¹ of it and would get X*(Y**0.5). Of course this can be generalized to arbitrary exponents.
An interesting case is the vector $(0, 1, 0, 0, \dots)$ which will shift all elements by one position in circular convolution. With non-integer exponents, it allows us to shift vector elements by partial positions!
These things are also mentioned in this internal tech report (towards the end, starting with the section “Circular auto-convolutions”). I probably also have some more precise notes about the math involved lying around if you are interested.
¹: I’m not sure out of my head whether actually halfing the angle and scaling is correct. As we are actually taking the exponential of a complex number, the mathematics get a little bit weird and normal power laws like (a**b)**c = a**(b*c) do not apply. The required math can be found here. The most relevant formula is probably $c^{k^m} = e^{m\cdot \mathrm{Ln}\ c^k} = c^{m(k - d [(1/2) + (k/d)])}$ where $\mathrm{Ln}$ is the principal value $\mathrm{Ln}\ z = \mathrm{Ln}\ |z| + i \mathrm{Arg}\ z$ and $[\cdot]$ is the floor function.
3 Likes
Sweet! So something like this should work:
def power(s, e):
x = np.fft.ifft(np.fft.fft(s.v) ** e).real
return spa.SemanticPointer(data=x)
That seems to behave as expected… power(s,2)==s*s and power(s,2.5).compare(s*s*s)==power(s, 2.5).compare(s*s)==0.64475
1 Like
Yep, seems like Python handles complex exponentiation. 
The internal tech report also gives you an analytic formula for the similarity using the shift-by-one vector that you can use to verify your results.
Hi,
Is it possible to retrieve the exponent? Let’s say I have a SSP ensemble that represents X**n and want to connect it to a 1-D ensemble that outputs n. If I understand the SSP article correctly, a traditional (and discrete) associative memory is used instead.
My attempt is not very stable non-neurally, and does not produce expected results neurally:
import nengo_spa as spa
import nengo
import numpy as np
dimensions = 64
vocab = spa.Vocabulary(dimensions)
vocab.populate("BASE.unitary()")
scale = 1.00001 # used to avoid log(1)
base = vocab.parse("BASE").v
def power(base, e):
return np.fft.ifft(np.fft.fft(scale*base) ** e)
def retrieve_e(y):
e = np.median(np.log(np.absolute(np.fft.fft(y))) / np.log(np.absolute(np.fft.fft(scale*base))))
if np.isinf(e): # happens while building with y=0
return 0
else:
return e
with spa.Network() as model:
e = nengo.Node([0])
trans = spa.Transcode(input_vocab=vocab, output_vocab=vocab)
state = spa.State(vocab)
state_out_ens = nengo.Ensemble(100*dimensions, dimensions)
trans.output.output = lambda t,x: x
exponent_ens = nengo.Ensemble(100,1,radius=10)
exponent_node = nengo.Node(size_in=1)
nengo.Connection(e, trans.input, function=lambda x: power(vocab.parse("BASE").v,x))
trans >> state
nengo.Connection(state.output, state_out_ens)
nengo.Connection(state_out_ens, exponent_ens, function=retrieve_e)
nengo.Connection(trans.output, exponent_node, function=retrieve_e)
Is there a better way to compute the exponent, both neurally and non-neurally?
Thanks in advance!
In general we find that often you can do things in SSP space without needing to retrieve n. For example, shifting the position, storing it in memory, or making spatial comparisons, can all be done in SSP space without decoding n. If as a last resort you need n represented as a scalar in an ensemble, you may be able to train a single layer to approximate this in specific regions of space, and given knowledge of X in the training data. @brent do you have some code for this somewhere?
By the way your retrieve_e function won’t work mathematically, because the complex exponential doesn’t have a well-defined inverse (it is a multivalued function with infinitely many branches).
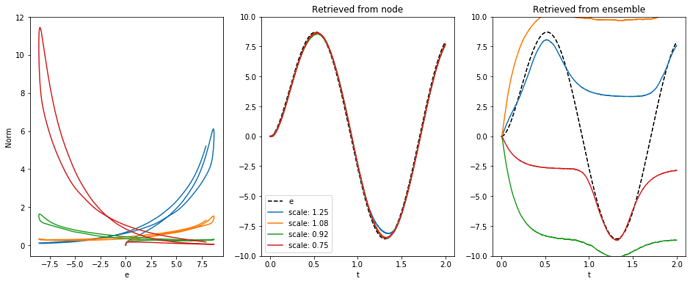
Thanks @arvoelke! That probably explains why I need to use this ugly scaling factor, which inevitably scales the exponentiated vectors up and down too.
I was actually about to post some updates. I am able to compute the exponent from a node using a small scaling factor. But it still doesn’t work well with neurons.
retrieve_exponent.ipynb (161.6 KB)
In my model, I use the SPAUN representation $DIGIT_N = ZERO*ADD_1**N$. My task is to determine whether a natural number N is larger or smaller than 5. And crucially, the response time should be inversely proportional to the distance between N and 5 (which is the reason why I cannot use an associative memory directly). I can easily implement this operation on a scalar representation, using the integrator network. Of course, I could use an associative memory to convert SSP into a scalar like you did in the article, but I was wondering whether a more general method could be used.
From my experience learning to convert an SSP to its coordinate works pretty well with neurons because SSPs exist in a very smooth space. For your example I would try setting the evaluation points explicitly. By default I believe Nengo will evaluate your function based on points within a sphere the size of your radius, but an SSP representing a 1D value just lives on a 1D manifold within that space, so the randomly chosen points as input to your function likely won’t look anything close to the SSP, making the function hard to learn. Here’s a quick snippet of doing this (from a 2D example, but 1D is similar):
train_vectors = np.zeros((n_samples, D))
train_coords = np.zeros((n_samples, 2))
limit = 5
for i in range(n_samples):
x = np.random.uniform(low=-limit, high=limit)
y = np.random.uniform(low=-limit, high=limit)
train_vectors[i, :] = encode_point(x, y, x_axis_sp=x_axis_sp, y_axis_sp=y_axis_sp).v
train_coords[i, 0] = x
train_coords[i, 1] = y
# ...
model = nengo.Network()
with model:
# ...
vector_input = nengo.Ensemble(n_neurons=D * neurons_per_dim, dimensions=D, neuron_type=nengo.LIF())
coord_output = nengo.Ensemble(n_neurons=200, dimensions=2, neuron_type=nengo.LIF(), radius=limit * 1.4)
nengo.Connection(
vector_input,
coord_output,
function=train_coords,
eval_points=train_vectors,
scale_eval_points=False,
)
As for ways to decode the coordinate without neurons, I found constructing a lookup table is a simple and quick way to get an approximation, and the same table can be used for plotting. Some code for generating the table is here and using it to retrieve coordinates is here.
@ikajic had worked out a more general way of retrieving the exact exponent (which might be similar to how you are doing it), though as @arvoelke mentioned it is a multivalued function, so you will have to decide on some range you care about.
1 Like
Looks like @brent gave pretty much the same answer I was going to! Here’s a quick implementation of exactly your task, though, and it looks like it works fine even with only 500 neurons:
import matplotlib.pyplot as plt
import nengo
import numpy as np
import nengo_spa as spa
D = 16
vocab = spa.Vocabulary(D, strict=False)
ZERO = vocab.parse('ZERO')
ADD_1 = vocab.parse('ADD_1')
def power(base, e):
return np.fft.ifft(np.fft.fft(base) ** e).real
v = ZERO*spa.SemanticPointer(power(ADD_1.v,2.3))
model = nengo.Network()
with model:
def stim_func(t):
p = (t%10)
v = ZERO*spa.SemanticPointer(power(ADD_1.v,p))
return v.v
stim = nengo.Node(stim_func)
ens = nengo.Ensemble(n_neurons=500, dimensions=D)
nengo.Connection(stim, ens)
output = nengo.Node(None, size_in=1)
n_samples = 1000
eval_points = []
result = []
for i in range(n_samples):
p = np.random.uniform(0, 10)
v = ZERO*spa.SemanticPointer(power(ADD_1.v,p))
eval_points.append(v.v)
result.append([1] if p>5 else [0])
nengo.Connection(ens, output, eval_points=eval_points, function=result)
p = nengo.Probe(output, synapse=0.01)
sim = nengo.Simulator(model)
with sim:
sim.run(10)
plt.plot(sim.trange(), sim.data[p])
1 Like
@brent @tcstewar Setting the evaluation points is a good idea. I will use that, thanks a lot! 
I’m curious if @ikajic has another working solution.
@tcstewar As for my task, I don’t think your code accounts for the differences in RT (see quote below). You also tried to capture this effect in this paper, but it seems that you used explicit evaluation points to learn the differences in magnitude directly.
Therefore, I will translate SSP into a scalar using the method with evaluation points, send the difference between the two digits to an integrator, and add the threshold as an output nonlinearity of the integrator. The integration process should take less time when the difference is larger, which is what you captured in your model.
Thanks again for your help!
Hi Hugo,
It’s been a long time since I played with this, but I managed to dig out a notebook that appears to have some sort of working code. As @arvoelke pointed out, there are multiple solutions and I remember having some heuristics to search for the plausible ones, but to be frank, I forgot what I did there. But maybe it is still somewhat useful (although I just tried running it and I can’t reproduce the same results for 2D 
). So, I can’t guarantee I’ll be able to immediately answer all your questions, but I will try my best.
Ivana
EDIT: I fixed the 2D case, it was querying a wrong list. I’ve tested the code for a few different combinations of coordinates (k1, k2) and it seems to be working now. Since I’m making a few assumptions here and there on ranges of values, I’ve also added some comments on what’s going on (my math notes are locked on campus so I don’t have the details here, but can probably reconstruct them if needed).
1 Like