Hi guys,
I had been getting some weird answers from my implementation of a model that does circular convolution with images and labels so I went back to basics, i.e. the circular convolution tutorial [here] (https://pythonhosted.org/nengo/examples/convolution.html), just adapting it to use arbitrary random vectors instead of the spa Vocabulary module. The output I get from the convolution network is sometimes close to the ground truth circular convolution but often it is not, and this changes from simulation to simulation.
Here’s the code to reproduce what I’m seeing:
import numpy as np
import nengo
from matplotlib import pyplot as plt
inputsize = 32
A = np.random.rand(inputsize)
B = np.random.rand(inputsize)
# just the ground truth circular convolution of A and B
C = np.real(np.fft.ifft(np.fft.fft(A)*np.fft.fft(B)))
model = nengo.Network()
with model:
nodeA = nengo.Node(output=A)
nodeB = nengo.Node(output=B)
cconv_ens = nengo.networks.CircularConvolution(200, dimensions=inputsize)
nengo.Connection(nodeA, cconv_ens.A)
nengo.Connection(nodeB, cconv_ens.B)
# Probe the output
out = nengo.Probe(cconv_ens.output, synapse=0.03)
with nengo.Simulator(model) as sim:
sim.run(1.)
plt.plot(sim.trange(), nengo.spa.similarity(sim.data[out], [A, B, C], normalize=True))
plt.legend(['A', 'B', 'C'], loc=4)
plt.xlabel("t [s]")
plt.ylabel("dot product between circular convolution out and A, B, and C");
plt.show()
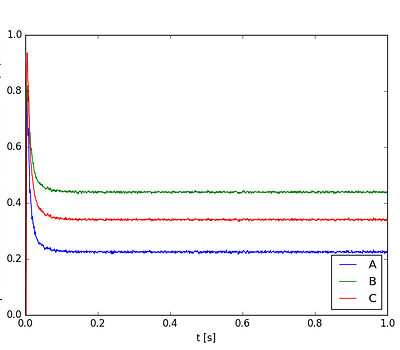
So just now I ran this and the first time the output was:
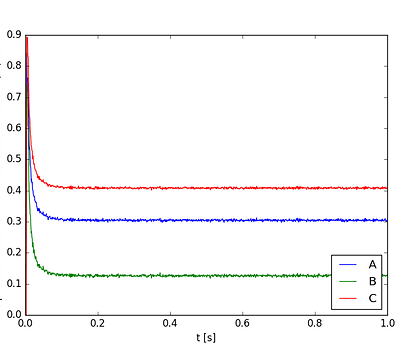
Not what i’m looking for. I ran it again and the output was
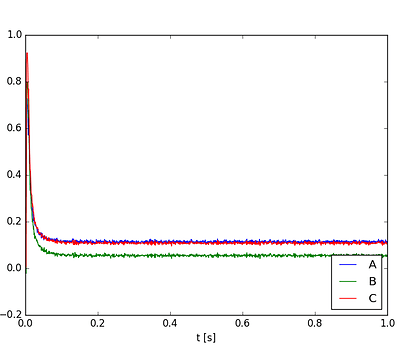
Now that’s more like it. Let’s try it a third time:
Hmmmm. This happens whether I’m on Nengo 2.1.2 or 2.2.0
Can you reproduce this and help me troubleshoot? Seems like maybe there’s a really simple answer I might be missing.
Spencer