Understanding pipeline of nengo/nengo_dl on hardware

General Discussion
1

Dear Nengo community,

I am trying to understand the nengo/nengo_dl pipeline. Just for an example let’s suppose we have a two-layer model with a single neuron in each layer.

image
image1161×200 5.2 KB

Once the model is trained and we want to run it on some hardware for instance loihi or FPGA. Then my understanding so far of the pipeline is:
Step 1: Given an input, it is multiplied first with the weight w1 and the product of this two is sent to the First layer LIF neuron.
Step 2: The LIF neuron based on the tunning_curve assigned spikes.
Step 3: These spikes are then decoded for the next layer? Am I correct? And based on the tunning_curve spikes are assigned to the decoded value. If my understanding is correct then how does this decoding looks like? Since I assumed everything after the first layer is done in spikes/current. How these spikes/currents are treated at next layer neurons?

Thank you in advance for your answer. :slight_smile:

2

Hi @Choozi,

If you are running it on hardware, the pipeline is typically hardware dependent. With respect to models run on hardware, Nengo and NengoDL merely serve to train the models to obtain the connection and neuron parameter weights needed for the network to perform some function. It is the responsibility of the respective backends (e.g., NengoLoihi, NengoFPGA, etc.) to then convert the network architecture (including the weights) into a structure that the hardware can natively use.

I’m not familiar with all of the hardware supported by Nengo, but most of the hardware apply the following pipeline to the neural network computation (using your 2 layer network as an example):

  1. Some input is provided. This input is multiplied by the connection weight matrix w1 and is fed into the first layer of LIF neurons. This input (that has been multiplied by the connection weight matrix) is treated as input current to the LIF neurons.
  2. For spiking neurons, the input current is fed into the neuron’s activation function. Depending on the state of the neuron (i.e., what the membrane voltage is, how much input current is being provided, etc.), the neuron may or may not generate a spike. Note that this is a “real-time” process. The membrane voltages are updated every timestep to determine if the neuron spikes or not.
    Note: For rate neurons, using the input current and the neuron’s response curve, a firing rate is computed (basically, the neuron’s response curve maps some input current to some output firing rate).
  3. The spikes generated by the first layer of neurons are filtered by a post-synaptic filter, and then multiplied with the connection weights w2. The post-synaptic filter “smooths” out the spikes and in combination with the connection weights “converts” the spike trains into input currents for the second neural layer.
  4. As with step 2, the input current from the previous step is fed into the second layer neuron’s activation functions which in turn generates (or not) spikes from the second layer.
  5. To get some output, the same post-synaptic smoothing is applied to the spike train of layer 2. These smoothed spike trains are multiplied with the weights w3 (also known as output weights) to generate the output signal.

You should note above that for spiking networks, the “communication” between each layer is a spike train. When the spike train “arrives” at the destination neuron, this is the point where the post-synaptic filter and the connection weight is applied. Also note that since the post-synaptic filter and the connection weights are just multiplicative (to be precise, the application of the post-synaptic filter is a convolution, and the application of the connection weights is a multiplication), the post-synaptic filter can be combined with the connection weights (i.e., scaling the post-synaptic filter), so the operation can be done in one step.

I should note that the terms “encoder” and “decoder” are pretty much only used in Nengo itself, and they may not physically exist in the hardware (unless the hardware is capable of doing computation using the NEF algorithm – i.e., the hardware is capable of using factorized weights). Rather, for some hardware, there only exists one “connection weight” matrix between neural layers. For such hardware, the respective Nengo backend would combine the encoders and decoders together to form the connection weight matrix.

3

Dear @xchoo,

Thank you very much for your prompt and detailed reply. I have few more questions to add.

  1. Some input is provided. This input is multiplied by the connection weight matrix w1 and is fed into the first layer of LIF neurons. This input (that has been multiplied by the connection weight matrix) is treated as input current to the LIF neurons.

How is this current calculated? Looking at different posts I came up with something this: “In Nengo a spike is a single timestep event with a magnitude of 1/dt. If you make a connection from a.neurons object, the resulting current fed to the post object depends on the synaptic filter applied on the connection. If the synapse is None or 0 , then no change to the spike is applied, and what is essentially a 1/dt single timestep spike of current is set to the post population. If a synapse is specified, the spike is convolved with the synapse, and that resulting current is sent to the post population (over time).”

My question is how much current a spike represents? Is this hardware specific?

  1. For spiking neurons, the input current is fed into the neuron’s activation function. Depending on the state of the neuron (i.e., what the membrane voltage is, how much input current is being provided, etc.), the neuron may or may not generate a spike. Note that this is a “real-time” process. The membrane voltages are updated every timestep to determine if the neuron spikes or not.
    Note*: For rate neurons, using the input current and the neuron’s response curve, a firing rate is computed (basically, the neuron’s response curve maps some input current to some output firing rate).

How this transition take place from rate neurons to spiking neurons? For instance, if the firing rate of a neuron is 100Hz then it means that when we translate it to a spiking neuron, the neuron will send a spike at every 10 milliseconds?

And we double the rate i.e., 200Hz then the spiking version of this neuron will spike every 5 milliseconds right?

I should note that the terms “encoder” and “decoder” are pretty much only used in Nengo itself, … connection weight matrix.

When I am using nengo_dl defining layers with keras does this include encoders and decoders as well?

4

The current is calculated literally as I described it – the input signal (be it from some exterior source, or as a spike train from a preceding neuron) is multiplied by some connection weight, then filtered by a synaptic filter. This process is consistent with the summary you quote in your question.

I must point out that there is a disconnect between the currents in Nengo and the currents found in biology. Nengo (as well as other neural network simulators) are abstractions of the processes found in biology, so there isn’t necessarily an exact mapping between Nengo and biology (i.e., 1 unit of current in Nengo doesn’t necessarily map onto 1 uA of current in biology).

A spike doesn’t represent current. A spike represents an instantaneous increase in voltage in some given timeframe. If you want to calculate the amount of current the spike represents, you’ll need to know the resistance of the axon the spike is travelling down (for physical systems). In Nengo, this resistance is not modelled (i.e., the resistance is 0), so using the formula I = \frac{V}{R}, we get that in Nengo, one spike has infinite current. For hardware like Loihi, spikes are typically digital signals (i.e., a ‘1’ being sent down a wire), so the amount of current contained in the spike depends on the hardware being used.

I should note that the amount of current contained in a spike is typically unimportant. The spike serves to inform the system that an event has occurred, and a current equal to the connection weight multiplied by some post-synaptic current (PSC) [the PSC is in turn determined by the synaptic filter being used] should be fed into the succeeding neuron.

In Nengo / NengoDL, converting a rate model to a spiking model typically involves just replacing the rate neurons with equivalently configured (i.e., same intercepts, same max rates, same refractory times, etc.) spiking neurons, all the while keeping the rest of the network unchanged.

When you do so, a rate neuron that was firing at 100Hz will spike with an inter-spike interval of 1/100s (10ms) at steady state. The “at steady state” qualifier here is very important because the firing rate equivalence assumes that the input to the neuron is constant. Unlike rate neurons (whose output firing rates can change very quickly), the internal dynamics of spiking neurons mean that they require time to process quick changes to their input, and this is the reason why spiking models are more noisy than rate models.

As a quick example, let’s say you have a rate neuron where the output firing rate is such (using 1ms timesteps): 100, 100, 100, 100, 100, 100, 100, 100, 100, 100, 200, 100, 100, 100 …
The spiking neuron equivalent would generate a spike after the first 10 timesteps, and (roughly) after the next 9 timesteps. If you calculate the effective spike rate of the spiking neuron, you’ll see that it’s just slightly over 100Hz, and the 200Hz jump seen in the rate neuron output completely disappears in the spiking case.

Yes, this is correct, but once again, with the caveat that it comparison is made at steady state.

No. The connections between neural layers in most NengoDL models are done between neuron objects. Making such a connection “bypasses” (i.e., does not use) the encoders and decoders. But, in the grand scheme of things, this is not important since encoders and decoders are abstract concepts used to solve for the connection weights (using the NEF algorithm), whereas with NengoDL, you are using Keras training methods to do the same thing (i.e., to solve for the connection weights).

5

@xchoo Thank you very much for taking the time to answer briefly. I would like to clear few more doubts…

Unlike rate neurons (whose output firing rates can change very quickly), the internal dynamics of spiking neurons mean that they require time to process quick changes to their input, and this is the reason why spiking models are more noisy than rate models.

Noisier here means that since it is not spiking at every time step that’s why it is noisy?

As a quick example, let’s say you have a rate neuron where the output firing rate is such (using 1ms timesteps): 100, 100, 100, 100, 100, 100, 100, 100, 100, 100, 200, 100, 100, 100 …

For this example, the rate-based neuron will send 1 spike every timestep till 10th-time step. At the 11th timestep it will send 2 spikes. Right?

In the spiking version of neuron, it will only send a single spiking at 11th time-step? and for the rest of the time steps it will be idle.

If you calculate the effective spike rate of the spiking neuron, you’ll see that it’s just slightly over 100Hz, and the 200Hz jump seen in the rate neuron output completely disappears in the spiking case.

Can you please elaborate it more?

But, in the grand scheme of things, this is not important since encoders and decoders are abstract concepts used to solve for the connection weights (using the NEF algorithm), whereas with NengoDL, you are using Keras training methods to do the same thing (i.e., to solve for the connection weights)

Does this mean that we are only changing the weights and biases in training when using the NengoDL. The gain and rest of the neuron parameters are not changed?

6

Spiking networks are typically noisier because information is only transmitted when a spike is generated. For example, if a rate network outputs this (with a 1ms timestep):

100, 100, 100, 100, 100, 100, 100, 100, 100, 100, 100, 100, 100, 100 …

The equivalent spike output would be:

0, 0, 0, 0, 0, 0, 0, 0, 0, 1000, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1000

I.e., 1 spike every 10 timesteps (note that the spike is 1000 in magnitude since it’s 1/dt). If you compare the rate and spike output, you can easily come to the conclusion that the spike output is much noisier than the rate network output.

It depends on how the neuron dynamics is implemented. For a neuron like the LIF neuron, there is a refractory period where the neuron doesn’t spike at all. More likely, what would happen is that the neuron spike at the 10th timestep, and then spike again at the 19th timestep (instead of the 20th timestep). This is what I mean by my statement:

If you look at the effective spike rate of the spiking LIF neuron would be 100Hz, then ~110Hz, then back to 100Hz. Comparing to the rate network though, the 200Hz jump doesn’t follow through to the spike output.

It depends on how you configure your NengoDL network. Typically, all of the neuron parameters will change. With respect to neuron parameters, there are really only two that define the behaviour of a (rate) neuron: the bias, and the gain. Biases, as you mentioned are separate inputs to the neuron and can be trained. Gains are typically rolled into the connection weights and so when the connection weights are changed, so to are the gains. Spiking neurons have additional parameters like the refractory time constant or the RC time constant, but those are not trainable.

Note that NengoDL operates somewhat differently from Nengo (core). In Nengo core, it is possible to get access to things like the gains and biases post-learning since the learning rules implemented in Nengo don’t typically changes those parameters. In NengoDL, however, since TensorFlow is used to train these networks, and since the gains and connection weights (encoders + decoders) are combined to form the TensorFlow equivalents before training, after training, it is possible that these individual components (encoders, decoders, gains) become inseparable from the overall connections weight value.

7

Dear @xchoo Thank you for your prompt reply and thank you for answering my question so patiently. I have some confusion back in my head that I would like to clear.

I.e., 1 spike every 10 timesteps (note that the spike is 1000 in magnitude since it’s 1/dt
). If you compare the rate and spike output, you can easily come to the conclusion that the spike output is much noisier than the rate network output.

I will try to explain my understanding with the following example. If we have a rate neuron with the following rates with a time step of 1ms

Rate neuron: 100, 100, 100, 100, 100, 100, 100, 100, 100, 100, 200, 100, 100, 100 , 100 , 100 , 100 , 100 , 100 , 100 …

Assuming no refractory period, the spiking equivalent would be:

Spike neuron: 0, 0, 0, 0, 0, 0, 0, 0, 0, 1000, 0, 0, 0, 0, 0, 0, 0, 0, 1000, 0
Right?

When we are looking at the rate neuron with 100Hz. So it will generate a spike every 10ms. So in the above example, the first spike will be on 10ms. Since at the 11th time step the rate is 200Hz this means now the second spike will be on 15ms. Now at 16ms, the rate is again 100Hz so the next spike will be generated at 25 ms as shown in the figure below.

image
image1007×366 3.71 KB

Is my understanding correct?

Now the spiking equivalent neuron. My understanding here is that 1/dt represents a threshold assuming that there is no refractory period. Right?

So the neuron will start accumulating for the 1st 9 steps as it reaches 1000 at the 10th time step It will spike. At the 11th time step, the rate is 200Hz and then again 100Hz so the next time 1000 will be achieved at the 19th time step, and hence it will spike. Then spike again on 29th step and so on…

image
image1007×367 3.77 KB

This is what my understanding is about rate neurons and spiking neurons.

In NengoDL, however, since TensorFlow is used to train these networks, and since the gains and connection weights (encoders + decoders) are combined to form the TensorFlow equivalents before training, after training, it is possible that these individual components (encoders, decoders, gains) become inseparable from the overall connections weight value.

So this means that we can represent the behavior of the neuron (with constant refractory and RC) by the connection weights and bias only? What I mean in this case I would only need the biases and weight connection to map it on FPGA.

One another question is about the training. When we are training in nengo_dl. During the training process is the neuron behavior like a conventional artificial neural network neuron? or is it a rate-based neuron?

Thank you very much for your patience :grimacing: and for answering my questions.

8

That is correct.

Ah… Here is where you go wrong. Rate neurons are so-called “rate” neurons because the output of the neuron is the current activity (firing rate) of the neuron. They don’t produce any spikes at all. Thus, if the rate neuron has an output firing rate of a constant 100Hz, the output of the neuron will be 100 in each timestep.

Spiking neurons, on the other hand, spike at the frequency determined by the activity of the neuron. Thus, if the output firing rate of a spiking neuron is 100Hz, they will spike every 10ms. Here’s a plot comparing the outputs of two identically configured neurons, one rate and one spiking:

image
image772×581 67 KB

In the plot, we see that, as expected, the rate neuron has a constant output of 100, whereas the spiking neuron spikes every 10 timesteps (the dt is 1ms). The inputs to both neurons are the identical. We also note that each spike in the spiking neuron output is 1/dt (which is expected). I should also note that these plots were generated in Nengo, and in Nengo, the data starts at t=dt, so the 5th timestep (for example) is at 0.006s and not 0.005s.

Now, let’s see what happens if the input is modified so that at the 11th timestep, the input value is increase so that the rate neuron should output 200 instead of 100. For the rate neuron, the change in the output should be immediate, since the rate neuron has no internal dynamics (i.e., no membrane voltages to calculate and propagate). For the spiking neuron, however, the sudden increase in the input will affect the output, but it takes time for the membrane voltage to accumulate and generate a spike. So, instead of an instantaneous change in the output, the second spike is generated at timestep 19 instead of 20.

image
image786×586 70.9 KB

If we were to calculate the effective firing rate of the spiking neuron, we see that for the first bit of the simulation, it’s 100Hz (spiking every 10ms). But for the second bit of the simulation, it’s ~111.11Hz (spiked at 9ms instead of 10ms). Compared to the rate neuron output, however, we see that the sudden spike to the input values is all but lost for the spiking neuron (only increased by 11Hz, whereas the rate neuron increased by 100Hz). This is what I meant when I stated:

If you want to experiment with this example, he’s the code I used to generate the plots. You can change the output of input_func to see how it affects the outputs of the neurons. There are some comments in the code which you should read careful. They tell you why certain values are set the way they are.
test_rate_spike_compare.py (3.5 KB)

This depends on the type of neuron used. For the LIF and ReLU neurons, this is the case (assuming the \tau_{ref} and \tau_{RC} values are the same on the FPGA as they are in the Nengo model). However, since the \tau_{ref} and \tau_{RC} values can be changed by the user, it’s typically better to transfer those values as well to the FPGA.

In NengoDL, the training process uses the rate-based version of whatever neuron type you have configured your network to use. Some machine learning software (e.g., TensorFlow), the “conventional artificial neural network neuron” is the rate-version of the linear neuron. There is no equivalent neuron type in Nengo, but the nengo.RectifiedLinear() neuron type closely approximates it (the activation of the linear neuron extends below 0Hz, whereas the rectified linear neuron stops at 0Hz).
Other machine learning software use ReLU neurons (identical to the nengo.RectifiedLinear() neuron), while others use TanH or Sigmoid neurons (both of these neuron types are also available in Nengo).

9

@xchoo Thank you very much and taking the time to briefly answer my questions. Thank you for the script. Although I understand the concept behind one spike, things get a bit confusing when there are multiple time changes in rate.

For instance, extending your example in the script, when I change the rate for 2ms i.e. keep it for 2 ms for 200 Hz, in the spiking domain the 2nd spike occurs around 19 ms as shown in the figure below.

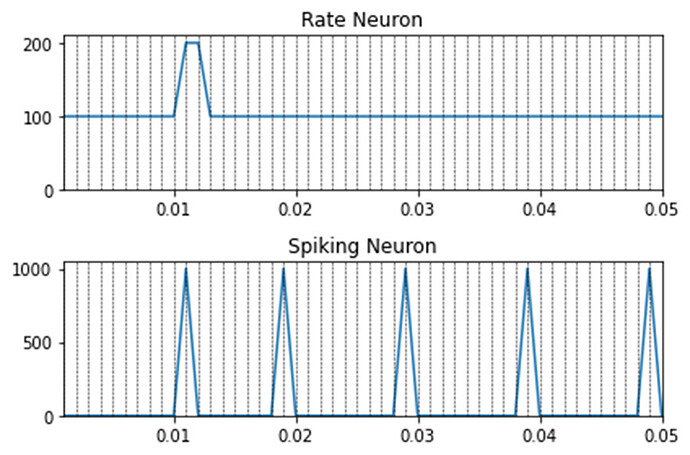
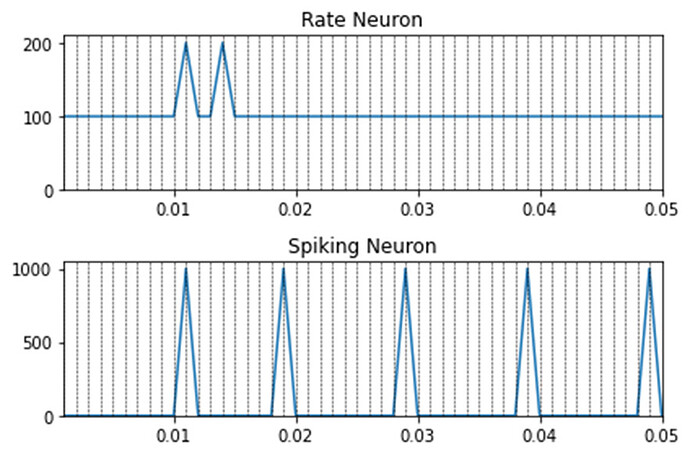
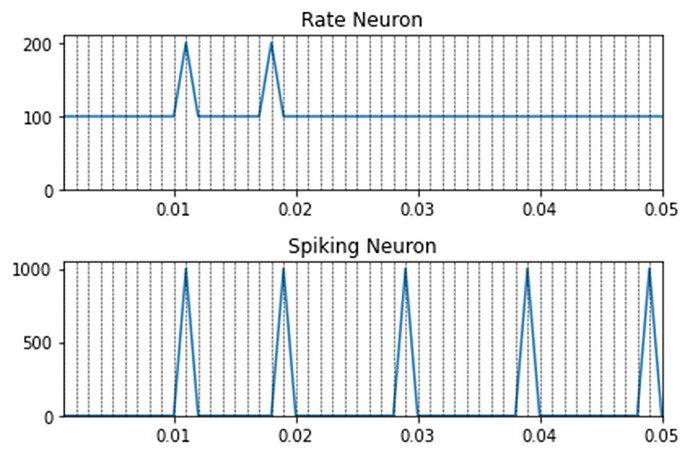
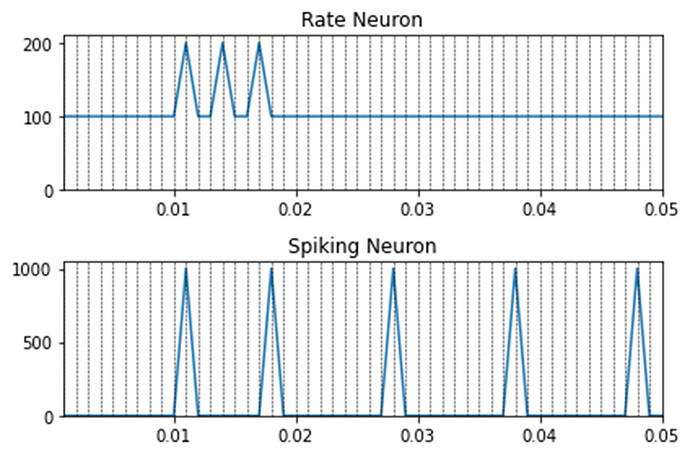
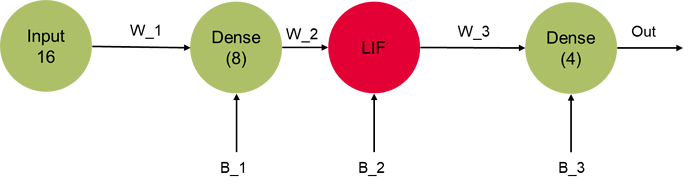
image
image883×583 102 KB

Now when I keep a 1 ms gap between two change rates, the behavior is the same in the spiking domain as shown below.

image
image883×583 102 KB

Similarly, if we have a change rate 11 ms and 18 ms the behavior in the spiking domain remain the same as shown below.

image
image883×583 102 KB

Now in case, we have three times change in rates in rate neurons, we have a second spike on 18 ms.

image
image883×583 103 KB

What I observed regardless of the location of the change of rates, every change in rate is causing 1 ms step (spike 1 ms earlier) in the spiking domain.

There must be some simple mathematical concept behind it that I fail to grasp. Can you please explain this behavior?

Thank you very much once again for answering my questions :slight_smile: and important for your patience. :grimacing:

10

If you look at the code for the rate LIF neuron, you’ll see that the output firing rate of the neuron is purely a function of the input current. That is to say, at every timestep, if you know what the input current to the neuron is, you can plug it into the mathematical formula to give you the output spike rate. This is analogous to having a short water pipe (facing down). If you pour 100ml into the pipe, it immediately exits the other end of the pipe. If you hook the pipe up to a faucet, the amount of water exiting the pipe will change as fast as you change how open/close the faucet is.

If you look at the spiking LIF neuron, on the other hand, you’ll see that the way Nengo determines if the neuron has spiked or not depends on the voltage (membrane voltage) of the neuron. If you follow the code, this membrane voltage is updated every timestep, but a spike is only generated when the membrane voltage cross a specific threshold (the spiking threshold). What this means is that there is no direct mapping between the input current and the output spike train. Rather, the input current causes the voltage to accumulate (i.e., integrate), and only when the voltage cross the spike threshold is a spike generated.

The spiking neuron activation function is analogous to having a bucket (or something like this fountain), rather than a short pipe. In this analogy, when the bucket overflows, a spike is considered to be “generated” (for the tipping fountain, when the bamboo thing tips over, that’s when a spike is generated). For a bucket, if you put 100ml into the bucket, it doesn’t necessarily overflow. In the examples above, where it takes 10 timesteps to generate a spike, it’s equivalent to putting 100ml into the 1L bucket at every timestep. After 10 timesteps, the amount of water in the bucket reaches 1L, and overflows, so a spike is generated.

We can use the pipe / bucket analogy to see how the rate and spike neurons will react to quick changes in the input current. For the rate neuron (pipe), a quick change to the input flow of water will result in an equally quick change in the output flow of water. But, for the spiking neuron (bucket), changing the input flow of water merely changes how fast the bucket fills. Thus, doing 200+200+100+100+100 ml of water (in 5 timesteps) is roughly equivalent to doing 200+100+100+100+200 ml of water (in 5 timesteps)**(see notes about LIF neurons at the end).That is why in your plots above, there is little difference between the first few plots. It’s only when you introduce a third 200Hz input does it impact the output firing rate (because an additional 200ml input will cause the bucket to fill faster).

A Note About LIF Neurons:
If you examine the name “LIF”, it stands for: Leaky-Integrate-and-Fire. The “integrate” part I’ve already explained, where the neuron integrates the input current (fills the bucket). The “fire” part I’ve also explained, where the neuron only fires when the membrane voltage reaches a specific value (the bucket overflows). The “leaky” part I haven’t yet explained. In the LIF neuron model, current actually slowly leaks out of the neuron. This is like having a small hole in the bucket. When you stop feeding the neuron with input current, the membrane voltage will slowly decay to 0. Likewise, if you stop putting water into a bucket that has a small hole in it, the water in the bucket will eventually slowly all leak out.

What this means is that there will be a difference in behaviour if you change when the input current is fed to the neuron. In the example plots you posted above, there actually should be a small difference in the case where you have 200Hz for timesteps 1+2 compared to 200Hz for timesteps 1+8. But, because the neuron is firing fairly fast compared to the dt of the simulation, this difference becomes lost (the dt is too large to resolve this small difference in spike times). If you reduce the firing rate of the neuron to 10Hz, or if you make the dt a smaller value (e.g., 10ns), you should see the difference pop up.

11

Dear @xchoo Thank you very much for taking the time and for the explanation. :slight_smile: You are simply great! :smiley:

One more thing I would like to clarify. When we are using nengo_dl.Layer in nengo_dl training. It only modifies the weight connection and the biases to the layer. However, when I extract the biases with get_nengo_params, it is different than the biases that are obtained with sim.keras_model.weights. Are the biases to the neuron layer and the biases of the LIF neurons two different things?

12

They should be the same. Although, because of the way weights are optimized in the underlying Keras model (for efficiency several bias weights can get combined together to form one big matrix), you may see different values if you compare the two (but the get_nengo_param weights should be contained somewhere in the keras_model.weights).

13

Dear @xchoo thank you for your prompt answer. Lets suppose the following example:

with nengo.Network(seed=0) as net:
    net.config[nengo.Ensemble].max_rates = nengo.dists.Choice([100])
    net.config[nengo.Ensemble].intercepts = nengo.dists.Choice([0])
    net.config[nengo.Connection].synapse = None
    neuron_type =nengo.LIF(amplitude = 0.01)
    # this is an optimization to improve the training speed,
    # since we won't require stateful behaviour in this example
    nengo_dl.configure_settings(stateful=False)

    # the input node that will be used to feed in input images
    inp = nengo.Node(np.zeros(16))

    x1 = nengo_dl.Layer(tf.keras.layers.Dense(8))(inp, shape_in=(1,16))
    x1 = nengo_dl.Layer(neuron_type)(x1)

    output = nengo.Probe(x1, label="output")    
    
    out = nengo_dl.Layer(tf.keras.layers.Dense(units=4))(x1)
    out_p = nengo.Probe(out, label="out_p")
    out_p_filt = nengo.Probe(out, synapse=0.01, label="out_p_filt")

When I print the weights before training:

Before training with get_nengo_params:
{'encoders': array([[ 1.],
       [ 1.],
       [ 1.],
       [ 1.],
       [-1.],
       [-1.],
       [-1.],
       [-1.]], dtype=float32), 'normalize_encoders': False, 'gain': array([2.0332448, 2.0332448, 2.0332448, 2.0332448, 2.0332448, 2.0332448,
       2.0332448, 2.0332448], dtype=float32), 'bias': array([1., 1., 1., 1., 1., 1., 1., 1.], dtype=float32), 'max_rates': Uniform(low=200, high=400), 'intercepts': Uniform(low=-1.0, high=0.9)}
Before training with sim.keras_model.weights:
[<tf.Variable 'TensorGraph/base_params/trainable_float32_8:0' shape=(8,) dtype=float32, numpy=array([1., 1., 1., 1., 1., 1., 1., 1.], dtype=float32)>, <tf.Variable 'TensorGraph/dense_25/kernel:0' shape=(16, 8) dtype=float32, numpy=
array([[-0.33486915,  0.40148127,  0.13097417, -0.06545389, -0.20806098,
         0.14250207,  0.4757855 , -0.06490052],
       [ 0.16010189,  0.10489583,  0.13663149,  0.11444879,  0.38933492,
         0.12776172,  0.03197503, -0.4740218 ],
       [-0.05912495, -0.24732924,  0.3862232 ,  0.38729346,  0.28728163,
        -0.44044805, -0.4289062 , -0.1915853 ],
       [-0.24881732,  0.4084705 , -0.02852035, -0.25761485,  0.13300395,
         0.08603108,  0.410012  ,  0.0701437 ],
       [-0.00356543,  0.0939151 ,  0.0414331 , -0.05708277, -0.20751941,
         0.23394465,  0.41970384,  0.16851854],
       [-0.28390443, -0.3134662 , -0.09283292, -0.49033797, -0.03442144,
        -0.20381367,  0.25012255,  0.02189696],
       [ 0.1371355 ,  0.06420732,  0.07077086, -0.47448373,  0.11151803,
        -0.1893444 , -0.01120353, -0.01354611],
       [-0.4414779 ,  0.39776003, -0.16403973,  0.41876316,  0.14977002,
         0.42905748, -0.07836056, -0.42671287],
       [ 0.26459813,  0.02045882, -0.33836246, -0.21259665,  0.18190789,
        -0.24045587, -0.40621114, -0.04324257],
       [ 0.30607176,  0.18740141,  0.21466279,  0.21725547, -0.30840743,
         0.17499697,  0.34543407, -0.20773911],
       [-0.40758514,  0.21844184, -0.20531535,  0.3941331 ,  0.2456336 ,
        -0.29453552,  0.28517365,  0.40464783],
       [-0.28130507,  0.21179736, -0.22052431, -0.40631115, -0.3692739 ,
        -0.34074497, -0.34367037,  0.34454226],
       [ 0.05650961,  0.03072739, -0.33571267, -0.33689427, -0.04421639,
        -0.15053117,  0.1564821 ,  0.4208337 ],
       [-0.39258194, -0.44293487, -0.22054589, -0.4338758 , -0.37818635,
        -0.04207456, -0.18798494, -0.03495884],
       [ 0.15310884,  0.15611696, -0.04791272,  0.39636707, -0.17005014,
        -0.279958  , -0.2546941 , -0.13452482],
       [-0.45635438, -0.22681558, -0.30091798, -0.16478252, -0.02208209,
        -0.23549163, -0.18475568, -0.08863187]], dtype=float32)>, <tf.Variable 'TensorGraph/dense_25/bias:0' shape=(8,) dtype=float32, numpy=array([0., 0., 0., 0., 0., 0., 0., 0.], dtype=float32)>, <tf.Variable 'TensorGraph/dense_26/kernel:0' shape=(8, 4) dtype=float32, numpy=
array([[ 0.01429349, -0.07985818, -0.12935376,  0.6964893 ],
       [ 0.26681113, -0.21800154, -0.09041494,  0.1429218 ],
       [-0.06134254,  0.3573689 , -0.44123855,  0.06895274],
       [ 0.06917661,  0.07004184, -0.31127587, -0.55301905],
       [ 0.18513662,  0.52865857,  0.04562682,  0.0864073 ],
       [-0.291421  ,  0.6059677 , -0.55191636,  0.6555473 ],
       [ 0.26294845, -0.30901057,  0.41675764, -0.56849927],
       [ 0.67330295,  0.47140473,  0.5104199 ,  0.23421204]],
      dtype=float32)>, <tf.Variable 'TensorGraph/dense_26/bias:0' shape=(4,) dtype=float32, numpy=array([0., 0., 0., 0.], dtype=float32)>]

After training the optimized weights are:

After training with get_nengo_params:
{'encoders': array([[ 1.],
       [ 1.],
       [ 1.],
       [ 1.],
       [-1.],
       [-1.],
       [-1.],
       [-1.]], dtype=float32), 'normalize_encoders': False, 'gain': array([2.0332448, 2.0332448, 2.0332448, 2.0332448, 2.0332448, 2.0332448,
       2.0332448, 2.0332448], dtype=float32), 'bias': array([0.99608827, 1.0442896 , 0.9583655 , 0.840119  , 0.8174738 ,
       0.9753371 , 1.1272157 , 1.1404463 ], dtype=float32), 'max_rates': Uniform(low=200, high=400), 'intercepts': Uniform(low=-1.0, high=0.9)}
After training with sim.keras_model.weights:
[<tf.Variable 'TensorGraph/base_params/trainable_float32_8:0' shape=(8,) dtype=float32, numpy=
array([0.99608827, 1.0442896 , 0.9583655 , 0.840119  , 0.8174738 ,
       0.9753371 , 1.1272157 , 1.1404463 ], dtype=float32)>, <tf.Variable 'TensorGraph/dense_25/kernel:0' shape=(16, 8) dtype=float32, numpy=
array([[-0.42222846,  0.24200168,  0.1228434 , -0.19200288, -0.21615249,
         0.22537254,  0.15830375,  0.14348662],
       [ 0.24897973,  0.24064443,  0.01594162, -0.01278597,  0.15329556,
         0.046916  ,  0.08096556, -0.27266836],
       [-0.47070235, -0.13800026,  0.347509  ,  0.11449179,  0.15270782,
        -0.66345483, -0.29918915, -0.1707631 ],
       [-0.5458111 , -0.04742003, -0.2862807 , -0.40992683,  0.25877243,
         0.07100935,  0.19473031,  0.14282067],
       [ 0.02363077,  0.4239431 , -0.01774568, -0.13983722, -0.3921473 ,
         0.29245335,  0.28123364,  0.0772593 ],
       [-0.47278467, -0.03457178, -0.14849444, -0.5372384 , -0.08720659,
        -0.32974714,  0.3656278 ,  0.07800148],
       [ 0.00100002, -0.3241698 ,  0.04821428, -0.43680564,  0.44487002,
        -0.18048719, -0.15704834,  0.13376418],
       [-0.5701078 ,  0.76006794, -0.22974566,  0.38979033, -0.09782179,
         0.38958353, -0.151282  , -0.47857407],
       [-0.04651041,  0.18091287, -0.41424903, -0.08234072,  0.2642943 ,
        -0.10087672, -0.45458052,  0.11325597],
       [ 0.21249026,  0.03274982,  0.3228077 ,  0.13583474, -0.36993992,
         0.3559691 ,  0.16389191, -0.16155171],
       [-0.51801544,  0.11881097, -0.08544519,  0.3828375 ,  0.0737737 ,
        -0.45559174,  0.09720748,  0.5586217 ],
       [-0.45184797,  0.18784086, -0.4561999 , -0.3188622 , -0.42621264,
         0.14698628, -0.55553156,  0.53076345],
       [-0.03956529, -0.10994054, -0.10967866, -0.3773059 , -0.24411117,
         0.03759727, -0.05840252,  0.36903772],
       [-0.41534385, -0.37392062, -0.26791674, -0.43218616, -0.5685533 ,
         0.10555435, -0.23374444,  0.01948378],
       [ 0.05834528,  0.2058212 , -0.2102371 ,  0.94866693,  0.12912013,
         0.20886466, -0.24586618,  0.02964282],
       [-0.4326087 , -0.35967124,  0.06181277, -0.40226054,  0.01146018,
         0.14308628, -0.4767727 , -0.09213054]], dtype=float32)>, <tf.Variable 'TensorGraph/dense_25/bias:0' shape=(8,) dtype=float32, numpy=
array([-0.00391253,  0.04429559, -0.04163574, -0.15988047, -0.18253754,
       -0.02466166,  0.12721722,  0.14045098], dtype=float32)>, <tf.Variable 'TensorGraph/dense_26/kernel:0' shape=(8, 4) dtype=float32, numpy=
array([[ 0.29734224, -0.04056702, -0.08777715,  0.3309865 ],
       [ 0.2889498 , -0.02732166, -0.20303652,  0.07589427],
       [ 0.3118579 ,  0.24252148, -0.542592  , -0.10831074],
       [ 0.11443946,  0.36353242, -0.6338987 , -0.592429  ],
       [ 0.11926413,  0.6897096 ,  0.03220635, -0.03515661],
       [-0.22724164,  0.48092696, -0.500028  ,  0.6807578 ],
       [ 0.00969276, -0.27644187,  0.5587347 , -0.4727213 ],
       [ 0.38449687,  0.6250343 ,  0.5408647 ,  0.32131493]],
      dtype=float32)>, <tf.Variable 'TensorGraph/dense_26/bias:0' shape=(4,) dtype=float32, numpy=array([-0.01315027, -0.02133778, -0.04621736,  0.10689242], dtype=float32)>]

You can see that the biases are changed when obtained with get_nengo_params compared to sim.keras_model.weights. But as you said that for efficiency the bias weights can get combined together to form one big matrix, considering this then if I have to put this neuron on the FPGA, what values I would use for the gain? By default, the gain of the LIF neuron is 1. Will I use the default values of the LIF neuron when a model with nengo_dl.Layer layers and trained with nengo_dl except for the bias that I will use the optimized one? or will I use the parameters I get with get_nengo_params. I hope I have explained my question well.

Thank you in advance for your answer. :slight_smile:

14

I’m not entirely sure I see this. After training, the bias values from get_nengo_params is:

'bias': array([0.99608827, 1.0442896 , 0.9583655 , 0.840119  , 0.8174738 ,
       0.9753371 , 1.1272157 , 1.1404463 ]

And from sim.keras_model.weights:

<tf.Variable 'TensorGraph/base_params/trainable_float32_8:0' shape=(8,) dtype=float32, numpy=
array([0.99608827, 1.0442896 , 0.9583655 , 0.840119  , 0.8174738 ,
       0.9753371 , 1.1272157 , 1.1404463 ], dtype=float32)>

And these are exactly the same values.

The other weight matrices are bias values for the other layers. Each layer in your network has an associated bias value.

In NengoDL, the gains should be rolled in with the connection weights, so you should be able to use just the connection weights for your FPGA model. I should note that the use of get_nengo_params does require you to get the handle on the Python objects that represent the ensembles and connection you want to probe. If you define your model as a “standard” Nengo network (i.e., using nengo.Ensemble, nengo.Connection, etc.), getting references to these Nengo objects is relatively straightforward.

But, since your model is defined in the TensorFlow style, I would use the weight obtained from sim.keras_model.weights instead. Just note that you’ll need to parse these weights yourself to figure out which ensemble (layer) and which connections they belong to.

15

@xchoo thank you for your reply.

I am sorry :man_facepalming:, I was comparing the biases of the neuron obtained with get_nengo_params:

‘bias’: array([0.99608827, 1.0442896 , 0.9583655 , 0.840119 , 0.8174738 ,
0.9753371 , 1.1272157 , 1.1404463 ]

with the biases connection weights to the neuron obtained with sim.keras_model.weights:

<tf.Variable ‘TensorGraph/dense_25/bias:0’ shape=(8,) dtype=float32, numpy=
array([-0.00391253, 0.04429559, -0.04163574, -0.15988047, -0.18253754,
-0.02466166, 0.12721722, 0.14045098], dtype=float32)>

and those are different.

This means that the Keras bias and the neuron bias are two different things. The connection to LIF neuron is the bias of the LIF neuron. What my understanding is that nengo trained in keras style will have the following pipeline considering one layer with one neuron.

image
image861×328 5.1 KB

So the input to the LIF neuron would be:

(input x weight + bias) x Neuron_bias

is this correct? while the gain of the neuron will not change in training.

But, since your model is defined in the TensorFlow style, I would use the weight obtained from sim.keras_model.weights instead. Just note that you’ll need to parse these weights yourself to figure out which ensemble (layer) and which connections they belong to.

I am working on it and will get back to you in case of questions.

Thank you very much once again for your prompt responses. :slight_smile:

16

No… I don’t believe this is the case. Like I mentioned in my previous post, each of the nengo_dl.Layer layers will have an bias input associated with it. When you do something like this:

x1 = nengo_dl.Layer(tf.keras.layers.Dense(8))

you are creating a layer of neurons with some TensorFlow default activation (I believe it’s ReLU, but I have to double check). Then, when you do this:

x1 = nengo_dl.Layer(neuron_type)(x1)

You are creating another layer of neurons, but this time, of neuron_type (which you set to nengo.LIF in your code).

So, for a network like that, it would look something like this:

        weight1              weight2
input ----------> Dense(8) -----------> LIF -----> Out
                     ^                   ^
                     |                   |
                   bias1               bias2

And in this case, all of the weights and biases are trainable.

EDIT: For correctness, I should point out that in NengoDL, weight2 is not trainable and is just an identity matrix. See my post below.

17

@xchoo Thank you for your prompt response. This is what I would think as well. But when I look at the weights obtained with sim.keras_model.weights then there are one connection weights missing to the LIF neuron. For instance, for the network below:

with nengo.Network(seed=0) as net:
net.config[nengo.Ensemble].max_rates = nengo.dists.Choice([100])
net.config[nengo.Ensemble].intercepts = nengo.dists.Choice([0])
net.config[nengo.Connection].synapse = None
neuron_type =nengo.LIF(amplitude = 0.001)
nengo_dl.configure_settings(stateful=False)

inp = nengo.Node(np.zeros(16))
x = nengo_dl.Layer(tf.keras.layers.Dense(8))(inp, shape_in=(1,16))
x = nengo_dl.Layer(neuron_type)(x)

# linear readout
out = nengo_dl.Layer(tf.keras.layers.Dense(units=no_of_classess))(x)
out_p = nengo.Probe(out, label="out_p")
out_p_filt = nengo.Probe(out, synapse=0.01, label="out_p_filt")

If I draw it would look like this:

image
image1314×355 10.3 KB

and the network weights I obtain with sim.keras_model.weights are:

[<tf.Variable ‘TensorGraph/base_params/trainable_float32_8:0’ shape=(8,) dtype=float32, numpy=
array([0.8269971 , 1.033082 , 0.96973974, 0.8842982 , 0.92986685,
0.9427234 , 1.2595564 , 1.1069744 ], dtype=float32)>, <tf.Variable ‘TensorGraph/dense_2/kernel:0’ shape=(16, 8) dtype=float32, numpy=
array([[-4.03423488e-01, 2.80470282e-01, 8.12819600e-02,
-4.18957859e-01, -2.56689459e-01, 5.97062372e-02,
1.96990326e-01, 1.20407835e-01],
[ 1.17101833e-01, 3.23715061e-01, 1.10586390e-01,
1.01157956e-01, 4.13867146e-01, 3.37027051e-02,
-7.93169588e-02, -5.31600237e-01],
[-2.63655037e-01, -1.67867377e-01, 1.27588645e-01,
2.26052627e-01, 9.81787816e-02, -6.93507791e-01,
-5.86813509e-01, -4.98261034e-01],
[-4.58302319e-01, -3.94521914e-02, 5.70545346e-03,
-2.91952431e-01, 2.44604304e-01, -2.97913607e-02,
3.22139829e-01, 2.66716361e-01],
[-2.36134365e-04, 4.98403430e-01, -1.25992540e-02,
2.11080024e-03, -3.23875129e-01, 4.28280950e-01,
1.71896949e-01, 9.99075919e-02],
[-4.62099195e-01, -2.30014563e-01, -2.24992171e-01,
-5.03440619e-01, -1.08375825e-01, -8.03755641e-01,
5.98352909e-01, 2.85588861e-01],
[ 2.03326028e-02, -1.23054639e-01, 2.70607024e-01,
-6.18643224e-01, 3.43336135e-01, -4.03545320e-01,
-8.36753249e-02, 1.53168261e-01],
[-4.55156982e-01, 9.92494643e-01, -9.45336297e-02,
7.18788624e-01, 3.10922176e-01, 7.51258433e-01,
-2.61553138e-01, -2.59839177e-01],
[ 8.06217343e-02, 1.84614822e-01, -5.17312825e-01,
-1.06743194e-01, -1.61632188e-02, -8.34572688e-02,
1.60860762e-01, 1.35708839e-01],
[ 2.14240879e-01, 4.00318727e-02, 4.80508119e-01,
-2.35948875e-03, -3.47393632e-01, 4.52014834e-01,
1.55317321e-01, -2.38284931e-01],
[-3.88102382e-01, 3.78434546e-02, 4.60461453e-02,
4.67765927e-01, 6.94859028e-02, -2.06781700e-01,
5.20673037e-01, 9.74633098e-01],
[-3.61382037e-01, 3.30238432e-01, -4.35587615e-01,
-4.13364708e-01, -6.60558641e-01, 2.35904872e-01,
-1.86940238e-01, 3.43034893e-01],
[-1.38514433e-02, -1.72108397e-01, -1.56204432e-01,
-6.99523389e-01, -2.36799866e-01, 9.48544443e-02,
-1.80083230e-01, 1.92503676e-01],
[-3.71393889e-01, -3.46228957e-01, -1.24921976e-02,
-3.28053117e-01, -5.42332947e-01, 3.09433788e-01,
-4.29382533e-01, 1.91020489e-01],
[ 5.31909280e-02, 4.50726211e-01, -2.11234704e-01,
7.06956089e-01, -1.28734902e-01, 2.25187466e-02,
-5.15594661e-01, -1.33257806e-01],
[-3.82450253e-01, -1.73353851e-01, -3.31455134e-02,
-3.10682654e-01, 5.87784685e-02, 4.40470397e-01,
-6.98478580e-01, -3.26493919e-01]], dtype=float32)>, <tf.Variable ‘TensorGraph/dense_2/bias:0’ shape=(8,) dtype=float32, numpy=
array([-0.17304705, 0.03313833, -0.03028677, -0.11569826, -0.07019567,
-0.0572703 , 0.2595916 , 0.10699787], dtype=float32)>, <tf.Variable ‘TensorGraph/dense_3/kernel:0’ shape=(8, 4) dtype=float32, numpy=
array([[ 0.09676459, -0.01773597, -0.17413993, 0.5595965 ],
[ 0.35248154, 0.07381734, -0.46754768, 0.12207104],
[ 0.2243698 , 0.40473473, -0.5966895 , -0.10875084],
[ 0.5741939 , 0.5621851 , -1.1698389 , -0.6847795 ],
[ 0.18858752, 0.73081934, -0.05109499, -0.02853805],
[-0.24761131, 0.6835108 , -0.9732872 , 0.9428548 ],
[ 0.16794077, -0.41437358, 0.8470477 , -0.8495212 ],
[ 0.61489314, 0.6719985 , 0.70173746, -0.10953254]],
dtype=float32)>, <tf.Variable ‘TensorGraph/dense_3/bias:0’ shape=(4,) dtype=float32, numpy=array([-0.02953565, 0.02043595, -0.02744072, 0.04174983], dtype=float32)>]

Looking at the weights:
TensorGraph/base_params/trainable_float32_8:0’ shape=(8,): is B_2
‘TensorGraph/dense_2/kernel:0’ shape=(16, 8) : is W_1
TensorGraph/dense_2/bias:0’ shape=(8,): is B_1
‘TensorGraph/dense_3/kernel:0’ shape=(8, 4): is W_3
TensorGraph/dense_3/bias:0’ shape=(4,): is B_2

Then W_2 is missing. Where can I extract it from?

Thank you.

18

In NengoDL, the connection between a TensorFlow layer (e.g., Dense) and a Nengo neuron-type layer does not contain any trainable weights. Nengo simply passes the outputs of the TensorFlow layer directly to the Nengo neuron layer with no changes. You can think of it as being a fixed identity matrix.

Thus, to answer your question, W_2 isn’t missing, it can be considered as just being transparent (i.e. has no applicable function).

19

Dear @xchoo thank you for your answer.

I am trying to reproduce the nengo_dl behavior within the layer however I am getting a mismatch in the spiking behavior.

I am attaching the notebook file and if you could please have a look at it and then let me know where I am making the mistake.
Test.ipynb (81.9 KB)

What I am trying to do is to implement the second layer activity with a simple python implementation. I take the input of the Nengo LIF CNN layer as the input to map it to the output of the dense layer. The output of the Nengo LIF Dense is used as a reference.

Could you please have a look at it and let me know what I am doing wrong?

Thank you very much in advance. :slight_smile:

20

@Choozi,
I didn’t have a lot of time to delve very deeply into your notebook, but if I had to guess, I think the discrepancy comes from the fact that the ReLU non-linearity (for the Dense layer) has not been taken into account when you do the manual computation. If you want confirm if this was the case, remove the Dense layer from the original network, re-save the weights, and redo the manual computation comparison again.