Hello,
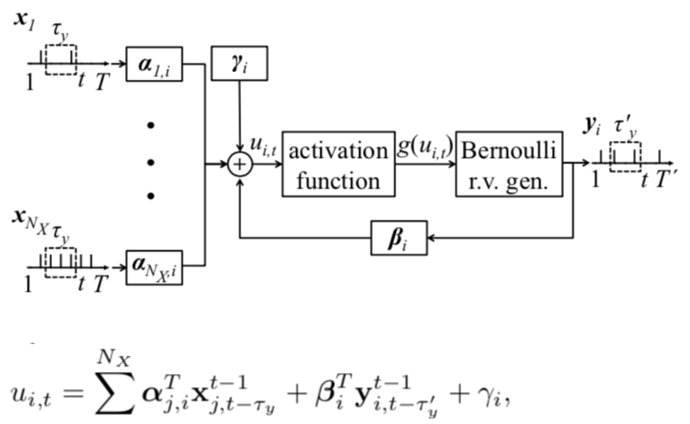
I am trying to construct a fully-connected 2-layer probabilistic SNN. The two layers are input layer and output layer. The neurons in the input layer receive the discrete-time spike train and the neurons in the output layer output the discrete-time spike train. The relationship between the two is based on the Generalized Linear Model. The membrane potential of a postsynaptic neuron at time t depends on the past spiking behaviour of the presynaptic neurons and the past spike output of the neuron itself.
where alpha, beta and gamma are the parameters I want to train.
I am still new to Nengo and could anyone give me some hints on how to construct this SNN and how to train it? Like is there any built-in functions which are useful?
Thanks in advance.
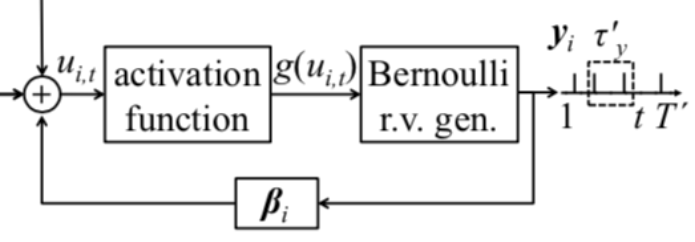
Generally the way to do this in Nengo currently is to create a custom neuron model that will handle everything from the “+” node, onwards, as in:
There are a couple examples on how to use random samples to generate a spike train, here: https://github.com/nengo/nengo/issues/1487. There is also a short tutorial on adding new objects to Nengo here: https://www.nengo.ai/nengo/examples/usage/rectified_linear.html.
For the rest of the drawing: The $\gamma_i$ term is supplied automatically by the ensemble, through its bias term. Likewise, the $\alpha$ terms are computed and supplied automatically by Nengo on the connection to the ensemble, through the product of the ensemble’s encoders, the presynaptic decoders (trained by Nengo), and the ensemble’s gain. You can also customize these terms by providing them to nengo.Ensemble. All of the resulting weights are generated automatically and solved for by connecting into the ensemble and specifying the function and transform.
Hi,
Thank you for your reply. When reading the tutorial on adding new objects, I can’t understand what gain_bias and max_rates_intercepts are doing. I know they should be specified according to the neuron but I am just confused about the underlying logic of gain, bias, max_rates, and intercepts.
Thanks in advance.
The logic of gain_bias and max_rates_intercepts are specific to the particular neuron model, providing a way of relating the distribution of weights (gain and bias as explained briefly in my last post) to some desired distribution of tuning curves. For example, with most neuron models in Nengo, one will typically specify a uniform distribution of intercepts tiled across [-1, 1], which correspond to the amount of normalized input current (i.e., unit-length vectors projected onto the encoders of the ensemble) required to make the neuron begin spiking. Meanwhile, one will typically specify a uniform distribution of max_rates, which correspond to the frequency of spiking for a normalized input current of 1 (again, unit-length vectors projected onto encoders). More details and pictures are available here: https://www.nengo.ai/nengo/examples/usage/tuning_curves.html.
In general, there will be some distribution of tuning curves that work well for the population, based on the space of inputs you’d like for it to represent, and the kinds of functions you’d like for it to support across that space. This distribution will have some correspondance with a multiplicative gain applied to each neuron’s postsynaptic weights, as well as the additive bias applied as an offset to each neuron’s input current. I would suggest exploring the Nengo documentation and referring to the source code for examples of how this is done for various neuron types. Let us know if you have a more specific question about something that you have tried or how this relates to your use case.
It might also be worth stepping back a bit and saying more about how you hope to train this network (online? offline? supervised? unsupervised?) and for what purpose (to fit some engineered function? classify some raw data?) and in what context (single-layer? multi-layer? recurrent?). Are there some learning rules that have already been devised for your use-case that you would like to explore? It may also be helpful to keep in mind that Nengo is a generic neural simulator that can be used to configure whatever starting point (i.e., architecture, neuron models, initial weights) that you would like, while allowing you to interface the model with various other mechanisms (i.e., online learning rules, and arbitrary Python nodes for input-output and other miscellaneous computations).
Hi,
I’d like to classify the MNIST by using a single-layer SNN. The input layer contains 28*28=784 neurons which receive the discrete train spike, and the output layer contains 10 Generalized Linear Models (GLM), which output the discrete train spike.
The detail of the GLM is:
https://forum.nengo.ai/uploads/default/original/1X/00199ccaac722840e840aea1337b2507eeea5dcd.png
Since the uit bases on both the input data during a certain time period and the output data during another certain time period, is it possible to train the three parameters (alpha, beta, gamma) in some way?
Thank you so much.
I tried to create a custom neuron model but it seems that it can only contain 2 parameters, that are gain and bias.
Thanks for the extra info, that certainly helps. Do you know if it’s necessary to train the three parameters (alpha, beta, gamma) for this task? Often we find that randomizing those parameters within some distribution, and then only training the readout weights (i.e., “decoders”) from the neural activity is sufficient – especially for datasets as simple as MNIST, but even for more complicated tasks like classifying surface textures by touch assuming appropriate encoding. The optimization that we typically perform in Nengo is this kind of training, where the “encoding” is fixed and the “decoding” is trained by solving for the optimal readout weights from the activities.
If you want to be able to train the encoding parameters then you need a method that can train across a layer, such as backpropagation. NengoDL allows you to take a Nengo model and then optimize it using TensorFlow for these purposes. Nengo also doesn’t force you to use any one kind of training method. If you have an alternate learning rule in mind, you can implement that learning rule in Nengo, either online or offline.
The two parameters of the custom neuron model (gain and bias) that you refer to are equivalent to the alpha and gamma parameters that we were talking about above. Typically we do not train these, but you could using NengoDL. The methods in the neuron model pertaining to gains and biases are simply relating these parameters to the distributions of tuning curves, so that Nengo can randomly initialize them. But you don’t need these methods if you’re not using them (i.e., if you manually specify initial values for gains and biases when you create the nengo.Ensemble). The beta parameter is more difficult to train since it is equivalent to the weight on a recurrent connection from each neuron back to itself. You could train beta by expressing the model as a recurrent neural network in NengoDL.