Greetings!
I followed the psmnist example on Nengo-dl and wanted to try using LMUs for a different time series classification problem. I picked the FordA binary classification problem to test my understanding of LMUs.
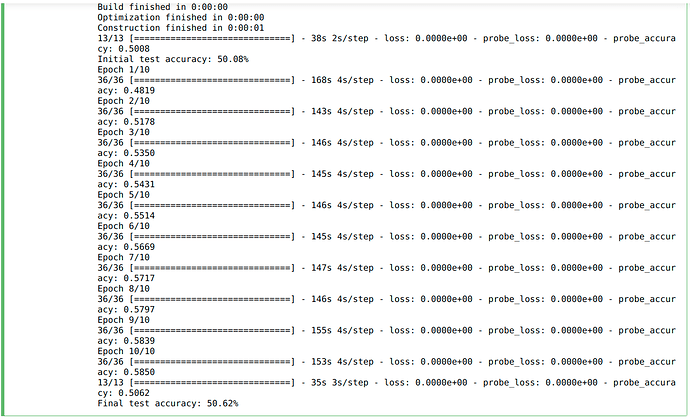
However, on training my LMU based network (similar structure as the one used in the psmnist example) for 10 epochs (same as the psmnist example), I got a final test accuracy of around 50% with little to no improvement between epochs.
This is the code I used (the first part is from the example I mentioned above)
import os
import tensorflow as tf
import numpy as np
import matplotlib.pyplot as plt
import tensorflow
from tensorflow import keras
def readucr(filename):
data = np.loadtxt(filename, delimiter="\t")
y = data[:, 0]
x = data[:, 1:]
return x, y.astype(int)
root_url = "https://raw.githubusercontent.com/hfawaz/cd-diagram/master/FordA/"
x_train, y_train = readucr(root_url + "FordA_TRAIN.tsv")
x_test, y_test = readucr(root_url + "FordA_TEST.tsv")
x_train = x_train.reshape((x_train.shape[0], x_train.shape[1], 1))
x_test = x_test.reshape((x_test.shape[0], x_test.shape[1], 1))
num_classes = len(np.unique(y_train))
idx = np.random.permutation(len(x_train))
x_train = x_train[idx]
y_train = y_train[idx]
y_train[y_train == -1] = 0
y_test[y_test == -1] = 0
#####nengo from here########################
import nengo
import nengo_dl
from nengo.utils.filter_design import cont2discrete
class LMUCell(nengo.Network):
def __init__(self, units, order, theta, input_d, **kwargs):
super().__init__(**kwargs)
# compute the A and B matrices according to the LMU's mathematical derivation
# (see the paper for details)
Q = np.arange(order, dtype=np.float64)
R = (2 * Q + 1)[:, None] / theta
j, i = np.meshgrid(Q, Q)
A = np.where(i < j, -1, (-1.0) ** (i - j + 1)) * R
B = (-1.0) ** Q[:, None] * R
C = np.ones((1, order))
D = np.zeros((1,))
A, B, _, _, _ = cont2discrete((A, B, C, D), dt=1.0, method="zoh")
with self:
nengo_dl.configure_settings(trainable=None)
# create objects corresponding to the x/u/m/h variables in the above diagram
self.x = nengo.Node(size_in=input_d)
self.u = nengo.Node(size_in=1)
self.m = nengo.Node(size_in=order)
self.h = nengo_dl.TensorNode(tf.nn.tanh, shape_in=(units,), pass_time=False)
# compute u_t from the above diagram. we have removed e_h and e_m as they
# are not needed in this task.
nengo.Connection(
self.x, self.u, transform=np.ones((1, input_d)), synapse=None
)
# compute m_t
# in this implementation we'll make A and B non-trainable, but they
# could also be optimized in the same way as the other parameters.
# note that setting synapse=0 (versus synapse=None) adds a one-timestep
# delay, so we can think of any connections with synapse=0 as representing
# value_{t-1}.
conn_A = nengo.Connection(self.m, self.m, transform=A, synapse=0)
self.config[conn_A].trainable = False
conn_B = nengo.Connection(self.u, self.m, transform=B, synapse=None)
self.config[conn_B].trainable = False
# compute h_t
nengo.Connection(
self.x, self.h, transform=nengo_dl.dists.Glorot(), synapse=None
)
nengo.Connection(
self.h, self.h, transform=nengo_dl.dists.Glorot(), synapse=0
)
nengo.Connection(
self.m,
self.h,
transform=nengo_dl.dists.Glorot(),
synapse=None,
)
y_test = y_test[:,None,None]
y_train = y_train[:,None,None]
seed=0
with nengo.Network(seed=seed) as net:
# remove some unnecessary features to speed up the training
nengo_dl.configure_settings(
trainable=None,
stateful=False,
keep_history=False,
)
# input node
inp = nengo.Node(np.zeros(1))
# lmu cell
lmu = LMUCell(
units=64,
order=256,
theta=x_train.shape[1],
input_d=x_train.shape[-1],
)
conn = nengo.Connection(inp, lmu.x, synapse=None)
net.config[conn].trainable = False
# dense linear readout
out = nengo.Node(size_in=1)
nengo.Connection(lmu.h, out, transform=nengo_dl.dists.Glorot(), synapse=None)
# record output. note that we set keep_history=False above, so this will
# only record the output on the last timestep (which is all we need
# on this task)
p = nengo.Probe(out)
do_training = True
with nengo_dl.Simulator(net, minibatch_size=100, unroll_simulation=25) as sim:
sim.compile(
optimizer=tf.optimizers.Adam(),
loss=tf.losses.CategoricalCrossentropy(from_logits=True),
metrics=["accuracy"],
)
print(
"Initial test accuracy: %.2f%%"
% (sim.evaluate(x_test, y_test, verbose=1)["probe_accuracy"] * 100)
)
if do_training:
sim.fit(x_train, y_train, epochs=10)
#sim.save_params("./lmu_params")
else:
urlretrieve(
"https://drive.google.com/uc?export=download&"
"id=1UbVJ4u6eQkyxIU9F7yScElAz2p2Ah2sP",
"lmu_params.npz",
)
sim.load_params("./lmu_params")
print(
"Final test accuracy: %.2f%%"
% (sim.evaluate(x_test, y_test, verbose=1)["probe_accuracy"] * 100)
)
Could you please help me figure out my mistake here.
Also, kindly suggest some sources for further intuition on LMUs and their hyperparameter tuning.