Update: This feature is now in nengolib>=0.4.2. This requires nengo>=2.5.0. The basic usage is:
nengo.Connection(..., solver=nengolib.Temporal())
The complete documentation (optional parameters, example, etc.) is currently hosted here: https://arvoelke.github.io/nengolib-docs/nengolib.solvers.Temporal.html#nengolib.solvers.Temporal
(Minor note: the order of the parameters has been swapped from the example below.)
In some situations it can be more accurate to explicitly simulate a population over time, collect its spiking activity, filter it, and then solve the least-squares problem on this data (as opposed to using the static rate-mode approximation). For instance, when using adaptive neuron models (e.g., AdaptiveLIF or Izhikevich), or, more generally, whenever the filtered spikes might convey more information than their corresponding rates.
Currently (as of Nengo 2.5.0), this takes considerable effort. The “standard” approach is to construct the entire model with a fixed set of seeds, simulate it, collect the training data, do the optimization yourself, reconstruct the model with the same seeds, and finally embed the new weights using a custom node or solver (see https://github.com/nengo/nengo/pull/1352 for instance). This can be tedious, inefficient, error-prone, and typically produces code that’s less modular. In practice, I’ve found that this “friction” will often deter me from applying this optimization to my own model.
To this end, this post demonstrates how to extend Nengo’s builder to have it automatically solve for the decoders by simulating the neurons over time (and filtering with some chosen synapse). This is enabled by simply wrapping whichever “underlying solver” you want (e.g., LstsqL2) with a custom solver (TemporalSolver; see below) when you create the connection. For instance,
nengo.Connection(..., solver=TemporalSolver())
defaults to LstsqL2 optimization, over time, with a 5 ms lowpass filter. The underlying solver and synapse may be passed as arguments to the TemporalSolver constructor. This makes it easy to quickly iterate, by testing this technique on some connections, without having to restructure the rest of your code, or perform multiple builds! Note, this uses the eval_points and function as you should normally expect, but the order of these points now matters – and you will likely want to filter the output of the function, using the same synapse, if your desired function is with respect to the unfiltered values (see example at very bottom).
This is currently only compatible with Nengo 2.5.0 and has not been extensively tested. Due to the way this has been implemented, this may not work with other backends, or in conjunction with other extensions to Nengo’s reference backend.
Please let me know if you have any issues, or if you can think of a better approach. And feel free to use/modify/redistribute, however you like, with or without attribution:
import numpy as np
import nengo
from nengo.builder import Builder
from nengo.builder.neurons import SimNeurons
from nengo.builder.signal import SignalDict
from nengo.config import SupportDefaultsMixin
from nengo.connection import ConnectionSolverParam
from nengo.params import Default
from nengo.solvers import Solver, LstsqL2
from nengo.synapses import SynapseParam, Lowpass
class TemporalSolver(Solver, SupportDefaultsMixin):
"""Wraps a solver to simulate the neurons over time."""
solver = ConnectionSolverParam(
'solver', default=LstsqL2(), readonly=True)
synapse = SynapseParam(
'synapse', default=Lowpass(tau=0.005), readonly=True)
def __init__(self, solver=Default, synapse=Default):
# We can't use super here because we need the defaults mixin
# in order to determine self.solver.weights.
SupportDefaultsMixin.__init__(self)
self.solver = solver
self.synapse = synapse
Solver.__init__(self, weights=self.solver.weights)
def mul_encoders(self, *args, **kwargs):
return self.solver.mul_encoders(*args, **kwargs)
def __call__(self, A, Y, rng=None, E=None): # nengo issue #1358
return self.solver.__call__(A, Y, rng=rng, E=E)
@Builder.register(TemporalSolver)
def build_solver(model, solver, conn, rng, transform):
# Unpack the relevant variables from the connection.
assert isinstance(conn.pre_obj, nengo.Ensemble)
ensemble = conn.pre_obj
neurons = ensemble.neurons
neuron_type = ensemble.neuron_type
# Find the operator that simulates the neurons.
# We do it this way (instead of using the step_math method)
# because we don't know the number of state parameters or their shapes.
ops = list(filter(
lambda op: (isinstance(op, SimNeurons) and
op.J is model.sig[neurons]['in']),
model.operators))
if not len(ops) == 1:
raise RuntimeError("Expected exactly one operator for simulating "
"neurons (%s), found: %s" % (neurons, ops))
op = ops[0]
# Create stepper for the neuron model.
signals = SignalDict()
op.init_signals(signals)
step_simneurons = op.make_step(signals, model.dt, rng)
# Create custom rates method that uses the built neurons.
def override_rates_method(x, gain, bias):
n_eval_points, n_neurons = x.shape
assert ensemble.n_neurons == n_neurons
a = np.empty((n_eval_points, n_neurons))
for i, x_t in enumerate(x):
signals[op.J][...] = neuron_type.current(x_t, gain, bias)
step_simneurons()
a[i, :] = signals[op.output]
return solver.synapse.filt(a, axis=0, y0=0, dt=model.dt)
# Hot-swap the rates method while calling the underlying solver.
# The solver will then call this temporarily created rates method
# to process each evaluation point.
save_rates_method = neuron_type.rates
neuron_type.rates = override_rates_method
try:
# Note: passing solver.solver doesn't actually cause solver.solver
# to be built. It will still use conn.solver. The only point of
# passing solver.solver is to invoke its corresponding builder
# function (in case something custom happens to be registered).
return model.build(solver.solver, conn, rng, transform)
finally:
neuron_type.rates = save_rates_method
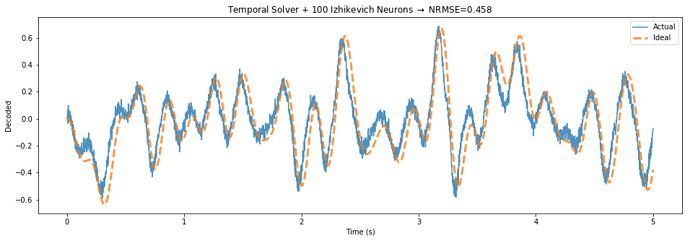
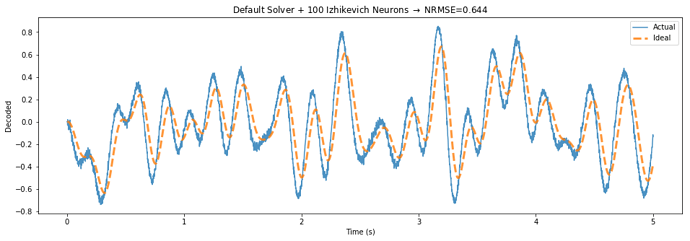
Below is a demo application that highlights the potential performance gains of this approach, by building a communication channel out of Izhikevich neurons.
The TemporalSolver takes 3 seconds to build on my machine, while the default solver takes over 100 seconds due to the way it processes each evaluation point. The normalized error decreases from 0.644 to 0.458 – a 29 percent reduction in error.
The only difference between the two figures is that the “Temporal Solver” uses a process to determine the activities over time, while the “Default Solver” determines the rate in response to each of these points independently.
import matplotlib.pyplot as plt
from nengolib.signal import nrmse
def demo(n_neurons=100,
dimensions=1,
neuron_type=nengo.Izhikevich(coupling=0.25), # low-threshold spiking (LTS)
synapse=nengo.Lowpass(0.01),
train_process=nengo.processes.WhiteSignal(10.0, high=5, y0=0, rms=0.3, seed=0),
test_process=nengo.processes.WhiteSignal(10.0, high=5, y0=0, rms=0.3, seed=1),
sim_t=5.0,
dt=0.001,
n_eval_points=5000,
temporal_solver=True):
"""Filtered communication channel demo."""
kwargs = {'eval_points': train_process.run_steps(n_eval_points, dt=dt, d=dimensions)}
if temporal_solver:
kwargs.update({
'solver': TemporalSolver(synapse=synapse),
'function': synapse.filt(kwargs['eval_points'], axis=0, y0=0, dt=dt)})
with nengo.Network() as model:
stim = nengo.Node(output=test_process, size_out=dimensions)
x = nengo.Ensemble(n_neurons, dimensions, neuron_type=neuron_type)
out = nengo.Node(size_in=dimensions)
nengo.Connection(stim, x, synapse=None)
nengo.Connection(x, out, synapse=None, **kwargs)
p = nengo.Probe(out, synapse=synapse)
ideal = nengo.Probe(stim, synapse=synapse)
with nengo.Simulator(model, dt=dt) as sim:
sim.run(sim_t)
plt.figure(figsize=(16, 5))
plt.title(r"%s Solver + %d %s Neurons $\rightarrow$ NRMSE=%.3f" % (
"Temporal" if temporal_solver else "Default",
n_neurons, type(neuron_type).__name__,
nrmse(sim.data[p], target=sim.data[ideal])))
plt.plot(sim.trange(), sim.data[p], label="Actual", alpha=0.8)
plt.plot(sim.trange(), sim.data[ideal], label="Ideal",
linestyle='--', lw=3, alpha=0.8)
plt.xlabel("Time (s)")
plt.ylabel("Decoded")
plt.legend()
plt.show()
if __name__ == '__main__':
demo(temporal_solver=True)
demo(temporal_solver=False)