Questions about membrane voltage update in a LIF neuron

[Tau]

Hi everyone,
Hi @xchoo,

I am trying to understand how the membrane voltage update is implemented in Nengo. I find the step function in Class LIF and read the source code. I am quite confused about a few lines in the source code.

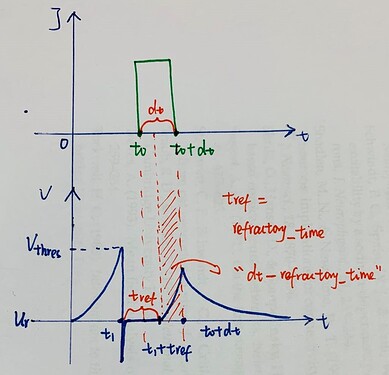
In the beginning, nengo updates the refractory_time and calculates the delta_t

658   # reduce all refractory times by dt
659   refractory_time -= dt
660   # compute effective dt for each neuron, based on remaining time.
661   # note that refractory times that have completed midway into this
662   # timestep will be given a partial timestep, and moreover these will
663   # be subtracted to zero at the next timestep (or reset by a spike)
664   delta_t = clip((dt - refractory_time), 0, dt)

My first question is why we need to subtract dt from refractory_time.

I know that if a neuron stays in its refractory_time, and it won’t react to any inputs. So, the time period where the neuron can take the input should somehow like “dt - refractory_time”.

Here is my second question. Considering that we do not know when dt starts and also refractory_time starts, why we can calculate the delta_t by dt - refractory_time.

The third question is about spike time

676   # set v(0) = 1 and solve for t to compute the spike time
677   t_spike = dt + tau_rc * np.log1p(
678                         -(voltage[spiked_mask] - 1) / (J[spiked_mask] - 1)
679                         )

I know that tau_rc * np.log1p( -(voltage[spiked_mask] - 1) / (J[spiked_mask] - 1)) is derived from v(t) = v(0) + (J - v(0))*(1 - exp(-t/tau)) and it is equal to -t. My question is that why we calculate t_spike using dt - t and what is the meaning?

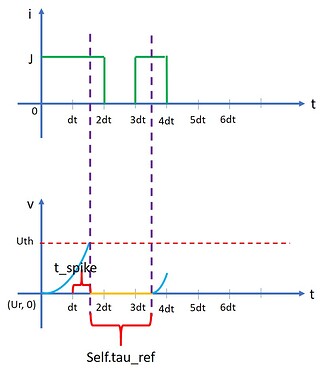
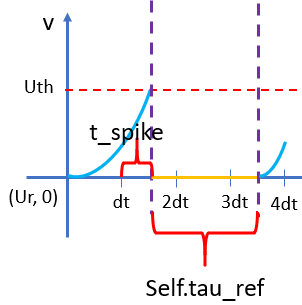
The last question is about the update of refractory_time.

685    refractory_time[spiked_mask] = self.tau_ref + t_spike

I do not understand why nengo updates refractory_time in this way.

Above, are my questions. Looking forward to your feedback~

[Eric]

Hi Tau, and welcome to the forum!

The refractory_time variable tracks how much time each neuron has remaining in its refractory period after a spike. So each step, we subtract dt (because time has advanced). If a neuron spikes, then we set the refractory period to tau_ref, plus a t_spike value that accounts for how much the neuron has “overshot” it’s threshold.

The t_spike value comes from the fact that we’re simulating things discretely, but it’s actually a continuous system. So let’s say a neuron’s voltage was at 0.8 the timestep before, and now is at 1.2, which is over its threshold of 1. This neuron spikes, but it didn’t actually spike right now, but a fraction of a timestep earlier when the voltage hit 1. We can compute how much earlier this neuron spiked. One simple way to do this would be linear interpolation; in our example, (1.2 - 1) / (1.2 - 0.8) = 0.5, so the neuron fired half a timestep earlier. However, since this is a first-order linear system, we can actually do better than linear interpolation and solve for the spike time exactly; you’ve noted correctly where this is derived from.

By adding this t_spike value to the refractory period, we can account for this amount of overshoot and lower the refractory period accordingly. (I know it looks like we add t_spike, where you might think we’d subtract it, but due to the fact that we subtract dt from refractory_period at the start of each timestep, combined with other details, means the math works out. You can either trust me on this or work through the details yourself.) One nice consequence of accounting for this overshoot is it allows us to represent firing rates whose periods are not an integer number of timesteps. For example, if you don’t account for overshoot (and have a hard voltage reset, where the voltage is set to 0 after a spike), if you drive a neuron so it should be firing at 750 Hz (assuming dt = 1 ms), which would be an input current around 0.75, then you’d actually end up with a neuron that just fires at 500 Hz. The first timestep, your voltage goes to 0.75, then to 1.5 where the neuron spikes and goes back to zero, and this just repeats, meaning you fire every second step i.e. 500 Hz.

[Tau]

Hi, @Eric ,

Thank you for reply. You really help me a lot. Now I have a better understanding about the logic in the source code in Class LIF. But I still a little bit confused(not much) about the code in line 659

659   refractory_time -= dt

In your reply, you mentioned that So each step, we subtract dt (because time has advanced). I am not quite sure about what time has advanced means.

I searched the assigned value for dt and self.tau_ref in the source code. I found that dt=0.001s and self.tau_ref = 0.002s. Obviously, self.tau_ref > dt. Besides, t_spike means how much earilier a neuron spikedhow long it takes a neuron to reach voltage threshold in a time step and, surely, dt > t_spike.

Based on these assumptions, I find that refractory_time[spiked_mask] = self.tau_ref + t_spike and refractory_time -= dt(in the next round) are to calculate the remaining refractory_time at the beginning of the following time step(also used to align with the beginning of time step). And surely, refractory_time > dt. So, the voltage of the spiked neuron stays at 0 in the following time step. In the following second time step, the refractory_time ends in the midway and the spiked neuron gets ready to receive the inputs.

I have drawn a diagram to illustrate what I mean. Feel free to correct me if there is anything wrong. Thanks a lot.

[Tau]

Hi，@Eric,

I think I have already figured out the timing problem in the Voltage Update Procedure.

I firstly need to point out that I misunderstood the meaning of t_spike. It should be the time for a neuron to reach the voltage threshold in a time step.

On important thing to understand the timing problem in Step function is that refractory_time -= dt is to update the refractory_time for the previous time step. delta_t = clip((dt - refractory_time), 0, dt) is to calculate the effective dt considering the remaining refractory_time for the current time step.

Thank you for your help.