I have nengo model and I need to add it some part that solves (non linear) optimization problem.
I need to find N dependent values that minimize some non linear objective.
Since I want to minimize the objective, I can’t use PES. I mean, something like PES, but instead of error, minimize objective. Is there such optimization solver in nengo?
Hi @nrofis,
From your problem description it seems like you might want to use NengoDL for your optimization problem, rather than just the standard Nengo. NengoDL allows you to train your Nengo networks similar to TensorFlow (in fact, NengoDL uses TensorFlow in the background). Note that NengoDL / TensorFlow is typically an off-line training method whereas the PES learning rule is on-line (i.e., as the network is being simulated).
Just to expand a bit here, there are two types of optimization that Nengo has built in. On the network level, you can optimize the network weights to compute a specific function by using the Nengo learning rules (PES, Oja, etc.). These learning rules optimize the network by trying to minimize an error value, and they do so as the simulation is running (i.e., as data is being presented to the network).
On the ensemble level, network weights are optimized to “compute” a specific function (more accurately, they approximate a specific function), using one of the Nengo solvers. These solvers try to find the network weights that best approximate the mapping between a set of evaluation points (by default, randomly generated – but you can also specify your own), and a function you want the ensemble to compute. This method optimizes the network weights in an off-line fashion, since the evaluation points don’t change as the simulation is running, and thus the network weights are “trained” when the network is built.
You might be able to use either of these methods for your optimization problem, if you can re-frame your optimization problem into one of these two situations. But, I think your best bet is to try out NengoDL and see if that will work better for you.
Thanks for the reply, but I don’t think its related to NengoDL. I don’t want to train a network, but use something similar to PES.
PES minimize an error online - if error is high, decrease the value. If the error is low, increase the value.
I want something similar to that, but instead of error, reduce some loss function or objective function.
For example, in a “regular programing” I would use `scipy.optimize.minimize" as a solver, not training a network…
I just want to use “neuromorphic optimizer solver” instead, if these is such thing…
Just to clarify, the PES learning rule works to minimize whatever is provided as the “error” signal. However, this “error” signal can be anything. For example, if you provide the PES learning rule with the pre-post (instead of post-pre), the PES learning rule would work to minimize this “error” signal, which is in turn maximizing post-pre.
With regards to your problem, if you can compute the loss or objective function based off the information that your network contains, then you can feed this value to the PES learning and it will work to minimize this value. This, in effect, will minimize the loss / objective function.
This is interesting since it is not that simple. I tried to do so, and this is the reason I opened this thead…
Say I have two ensembles A and B which encodes constant value of 0. My goal is to find decoders that will being a values that minimize A^2+B^2+(A+B-0.5)^2. The optimal solution is decoders that brings both A and B to something around 0.2.
But using this objective function as PES input, not working. The objective function is always positive, so PES see a positive error and bring A and B down (instead up). At the end, PES finds decoders that brings both A and B to -1, and the cost function is much higher than the original value, which is wrong…
How can I find the right decoders that minimize that objective function?
You are correct in the observation that for the specific objective function A^2 + B^2 + (A+B-0.5)^2, applying it naively to the PES rule will not work. This is because this specific function is always positive. Worse still, at the minima of the objective function, the value is non-zero. For other readers that want to know why this is an issue, I’ve explained it further down in this post.
In order to build a working system then, you’ll need to reframe the PES error value such that it has a positive and negative value, depending on which way you need the decoders to be adjusted. For this objective function in particular, the gradients (partial derivatives) of each variable in the objective function can be used to provide such a signal. The gradient is particularly useful in this scenario because the objective function is at a minimal value when the derivative of it is 0. Additionally, the gradients have the right sign, where a negative gradient should drive up a value, and a positive gradient should drive down a value.
For your particular problem, using the gradient as the PES error signal is straightforward. Changes to the value of A should be driven by \frac{\partial f}{\partial A}, and changes to the value of B should be driven by \frac{\partial f}{\partial B}. You can implement this in Nengo multiple ways, either with one ensemble each representing A and B, or you can have one 2D ensemble representing both A and B. Other than that, all you need to do is to compute the partial derivatives, and use the result as the learning rule error signal. If you have two ensembles for A and B, you’ll need two connections and two error signals. If you used one ensemble, you can combine both partial derivatives into one 2D error signal. In the code snippet below, I’ve used an ensemble each for A and B.
import nengo
def part_A_func(x):
return 4 * x[0] + 2 * x[1] - 1
def part_B_func(x):
return 4 * x[1] + 2 * x[0] - 1
with nengo.Network() as model:
ensA = nengo.Ensemble(50, 1)
ensB = nengo.Ensemble(50, 1)
out = nengo.Ensemble(100, dimensions=2)
conn1 = nengo.Connection(ensA, out[0])
conn1.learning_rule_type = nengo.PES()
conn2 = nengo.Connection(ensB, out[1])
conn2.learning_rule_type = nengo.PES()
nengo.Connection(out, conn1.learning_rule, function=part_A_func, synapse=0.1)
nengo.Connection(out, conn2.learning_rule, function=part_B_func, synapse=0.1)
part = nengo.Node(size_in=2)
nengo.Connection(out, part[0], function=part_A_func, synapse=0.1)
nengo.Connection(out, part[1], function=part_B_func, synapse=0.1)
p_out = nengo.Probe(out, synapse=0.1)
p_part = nengo.Probe(part)
with nengo.Simulator(model) as sim:
sim.run(10)
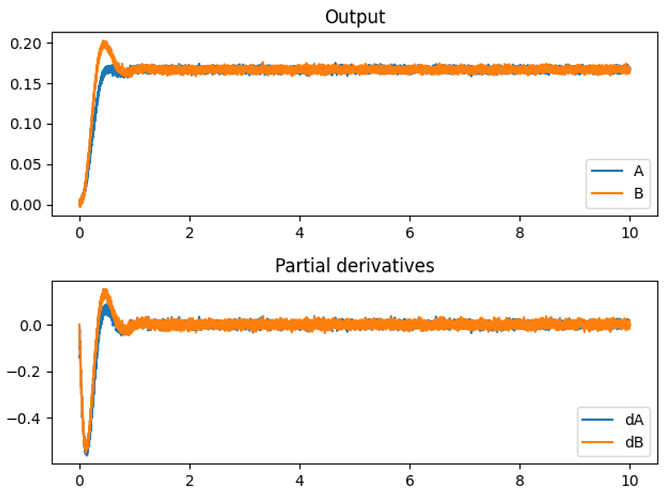
If we run this code, we get a plot like so:
And from this plot, we can see that the system does converge to approximately the correct values – according to Wolfram Alpha, the objective function is minimized when A=1/6 and B=1/6.
Now, this approach may not always work, and is dependent on the objective function used. Regardless, the key takeaway from this exercise is that to get around the limitations of the objective function (i.e., it never going negative), one needed to reframe the problem and find a way to generate error signals that could be used with the PES learning rule.
Side note: Why an always-positive error signal is bad for the PES
The PES learning rule works by modifying the decoders of a Nengo connection in the direction opposite of the error signal. I.e., if the error signal is positive, the decoded output of the learned population will be driven in the negative direction (and vice versa for a negative error value). This behaviour poses an issue if the function used to calculate the error signal is always positive for the range of values it is trying to optimize over.
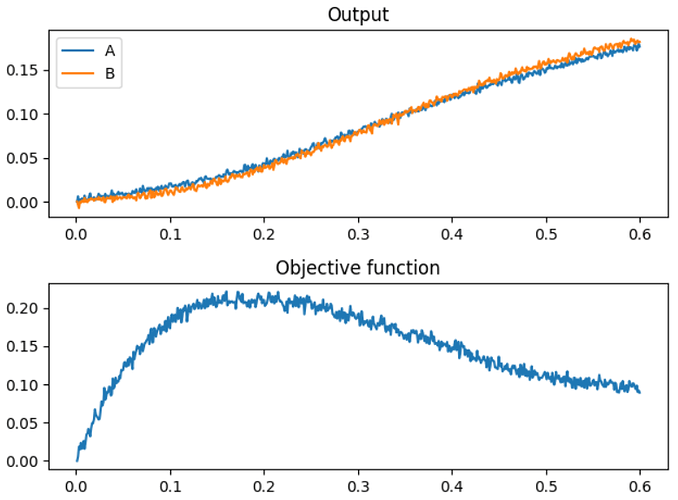
Take the objective function above (A^2 + B^2 + (A+B-0.5)^2) as an example. If we were to use the negative output of the objective function as the input to the “error” signal of the PES learning rule, it would initially do as expected. That is to say, it would increase the represented values of A and B in order to reduce the error value, as demonstrated by this plot:
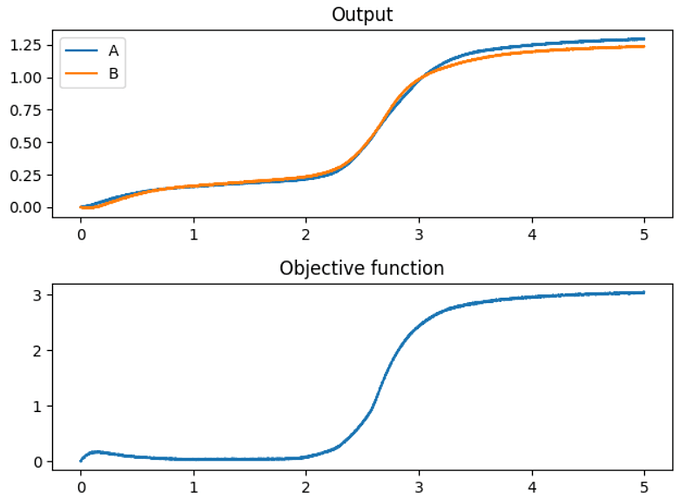
However, once the objective function reaches it’s minimum value (when the objective function is equal to 1/12), it is still positive, which means that rather than the PES learning rule stopping (ideally it should stop when the minima is reached), the PES error would continue to increase the values of A and B in an attempt to continue decreasing the output of the objective function. However, this just works to increase the output of the objective function, which creates a positive feedback loop, forever increasing the values of A and B:
Thank you so much @xchoo. Actually, it would be cool to implement a learning rule that does that automatically even for more complex objective functions that their derivative is not straight forward, like other optimization solvers. But this is more than enough for me! Thanks!
Another thing is that your implementation is a simple gradient descent algorithm. Which may not work so well for a more complex objective function.
