I have a quick question on “tuning curves”
Lets consider to have all inputs = sequences from a EMG device
activation = Relu, and using model.keras we can get layer wise activation vs input,
But how to know which tuning pattern is required for finding preferred directional curves like this (On the relations between the direction of two-dimensional arm movements and cell discharge in primate motor cortex - PubMed) 1982 literature?
Hi @ssp
This question is rather vague, so it is a little difficult to answer. The short answer is that without knowledge of the task from which the EMG was recorded, there is no way to know for sure what the tuning curves for the recorded data looks like. For the paper you cited, there was a hypothesis that the neurons being recorded represented the 2D arm movements in some way, so the spike data could be analyzed to see if this was the case (i.e., if there is a correlation between spiking activity and some vector in 2D space).
You can do the same thing with your data as well. If you have a hypothesis as to the dimensionality of the information being represented by the EMG, you can do principle components analysis (or some other similar technique) to identify the dimensions which best represent your data.
An aside about tuning curves: In Nengo, when you create an ensemble, you (the user) has to specify the dimensionality of the ensembles, and this in turn determines the dimensionality of the tuning curve. In TensorFlow (Keras), the tuning curves come about as a mix of the shape of the signals being processed as well as the connection weights determined by the learning algorithm.
Sorry I forgot to provide the paper.
I am experimenting on this paper ( On the relations between the direction of two-dimensional arm movements and cell discharge in primate motor cortex - PubMed) and trying to find the cosine tune for arm movements.
So I have all 8 angles as target and activity of individual neurons from Keras sequential model.
I am new to neuro analysis so Kind of confused about how to plot the “cosine tuning curve mentioned in figure 4 (paper)”
Your question isn’t strictly a Nengo-related question, but I’ll do my best to answer it.
To obtain the cosine tuning curve, what the authors did was to record from 1 neuron in the motor cortex as the monkey was doing reach tasks. For each position (location) of the target, they calculated the average firing rate of that particular neuron for that target position. Since the targets were on a 2D plane, you can consider the target’s position (i.e., xy coordinate) as some angle $\theta$ from some reference point. As an example if you choose straight up as 0 degrees, a target that is directly to the right would be 90 degrees. You can then plot the recorded neuron firing rate at each of these target angles on a graph, and what you should get is the cosine tuning curve.
You can do a similar thing with your Keras model. All you would need to do is feed the model different values of the target location, and probe the neuron firing rate for each location. Then you can plot the neuron firing rate vs the target location (angle) to get your cosine tuning curve.
Doing a Google search for “plot cosine tuning curve” I came across this PDF document that may be helpful to you.
As a note, this forum is mostly for Nengo related questions, and for general neuroscience / psychology questions, you would get a better response on other resources. I will suggest posting general neuroscience / psychology questions on something like Stack Exchange (for psychology), or some place similar. 
Thank you so much for the reference, It helped.
But I followed this code Nengo/nengo_test1.ipynb at main · alekshex/Nengo · GitHub but i dont understand why the loss is really huse.
from sklearn.metrics import mean_squared_error
from math import sqrt
def RunNetwork(
model,
inputTest,
outputTest,
activation,
params_file="./nengo-model-relu-1",
n_steps=30,
scale_firing_rates=1,
synapse=None,
n_test=15000,
):
# convert the keras model to a nengo network
nengo_converter = nengo_dl.Converter(
model,
swap_activations={tf.nn.relu: activation},
scale_firing_rates=scale_firing_rates,
synapse=synapse,
)
inputLayer = model.get_layer('input_5')
hiddenLayer1 = model.get_layer('dense_13')
outputLayer = model.get_layer('dense_14')
# get input/output objects
nengo_input = nengo_converter.inputs[inputLayer]
nengo_output = nengo_converter.outputs[outputLayer]
# add a probe to the first layer to record activity.
# we'll only record from a subset of neurons, to save memory.
sample_neurons = np.linspace(
0,
np.prod(hiddenLayer1.output_shape[1:]),
100,
endpoint=False,
dtype=np.int32,
)
with nengo_converter.net:
probe_l1 = nengo.Probe(nengo_converter.layers[hiddenLayer1][sample_neurons])
# repeat inputs for some number of timesteps
testInputData = np.tile(inputTest[:n_test], (1, n_steps, 1))
# set some options to speed up simulation
with nengo_converter.net:
nengo_dl.configure_settings(stateful=False)
# build network, load in trained weights, run inference on test
with nengo_dl.Simulator(
nengo_converter.net, minibatch_size=100, progress_bar=False
) as nengo_sim:
nengo_sim.load_params(params_file)
data = nengo_sim.predict({nengo_input: testInputData})
# compute accuracy on test data, using output of network on
# last timestep
predictions = np.argmax(data[nengo_output][:, -1], axis=-1)
#accuracy = (predictions == outputTest[:n_test,0]).mean()
#print("Test accuracy: %.2f%%" % (100 * accuracy))
n = 66
t = outputTest[:n_test]
t1 = t[:-n, :]
print(t1.shape)
#newarr = data[nengo_output].reshape(2200,30*9)
#print(newarr.shape)
#idx_IN_columns = [0,1,2,3,4,5,6,7,8]
# extractedData = newarr[:,idx_IN_columns]
#print(extractedData.shape)
#mse = mean_squared_error(t1, extractedData)
mse = mean_squared_error(t1, data[nengo_output][:n_test, -1]) #normalized comparison
print('\nMSE Nengo run net prediction of {} samples: {}\n\n'.format(n_test, mse))
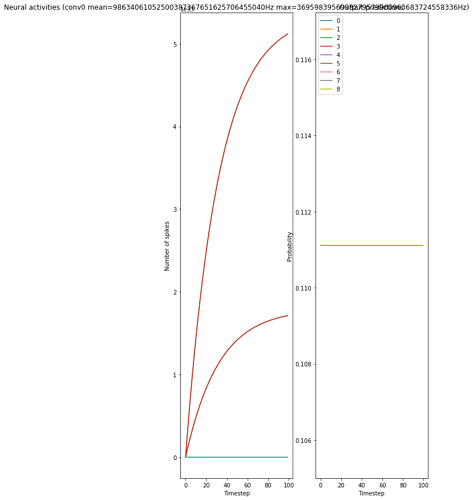
# plot the results
for ii in range(3):
plt.figure(figsize=(12, 15))
plt.subplot(1, 3, 1)
scaled_data = data[probe_l1][ii] * scale_firing_rates
if isinstance(activation, nengo.SpikingRectifiedLinear):
scaled_data *= 0.001
rates = np.sum(scaled_data, axis=0) / (n_steps * nengo_sim.dt)
plt.ylabel("Number of spikes")
else:
rates = scaled_data
plt.ylabel("Firing rates (Hz)")
plt.xlabel("Timestep")
plt.title(
"Neural activities (conv0 mean=%dHz max=%dHz)" % (rates.mean(), rates.max())
)
plt.plot(scaled_data)
plt.subplot(1, 3, 2)
plt.title("Output predictions")
plt.plot(tf.nn.softmax(data[nengo_output][ii]))
plt.legend([str(j) for j in range(10)], loc="upper left")
plt.xlabel("Timestep")
plt.ylabel("Probability")
plt.tight_layout()
Model: "model_4"
_________________________________________________________________
Layer (type) Output Shape Param #
=================================================================
input_5 (InputLayer) [(None, 8)] 0
_________________________________________________________________
dense_12 (Dense) (None, 50) 450
_________________________________________________________________
dense_13 (Dense) (None, 50) 2550
_________________________________________________________________
dense_14 (Dense) (None, 9) 459
=================================================================
Total params: 3,459
Trainable params: 3,459
Non-trainable params: 0
_________________________________________________________________
Build finished in 0:00:00
Optimization finished in 0:00:00
Construction finished in 0:00:00
Epoch 1/50
60/60 [==============================] - 2s 10ms/step - loss: 123382645707592641153086676315144192.0000 - probe_loss: 123382645707592641153086676315144192.0000 - val_loss: 2436953723512029184.0000 - val_probe_loss: 2436953723512029184.0000
Epoch 2/50
60/60 [==============================] - ETA: 0s - loss: 3139064446324760576.0000 - probe_loss: 3139064446324760576.00 - 0s 5ms/step - loss: 3144638822838040576.0000 - probe_loss: 3144638822838040576.0000 - val_loss: 2436953723512029184.0000 - val_probe_loss: 2436953723512029184.0000
RunNetwork(
NNa,
inputTestNgo,
outputTest,
activation=nengo.SpikingRectifiedLinear(),
params_file="./nengo-model-relu-1",
n_steps=100,
synapse=0.032,
scale_firing_rates=1500,
#n_test=100
)
