NengoDL MNIST Tutorial: Effect of amplitude on accuracy

[Choozi]

Hello Nengo community,

I am trying to understand the effect of the LIF neuron amplitude in the MNIST tutorial.

I am changing the amplitude of the neuron from 0.01 to 0.5 with step 0.01 with the following settings:

net.config[nengo.Ensemble].max_rates = nengo.dists.Choice([100])
net.config[nengo.Ensemble].intercepts = nengo.dists.Choice([0])
net.config[nengo.Connection].synapse = None

According to my understand:

1)The first line sets the neuron max firing rate to 100 Hz, right? or it is randomly with max to 100?
2) The intercept is the intercept for a neuron to start firing, am I right?

Now coming to the main questions. Changing the amplitude of the neuron gives me the following accuracy plot.

Why is this behavior like this? why is the zig-zag behavior of the accuracy with increasing the amplitude?

Thank you in advance for your answer.

[xchoo]

@Choozi

1)The first line sets the neuron max firing rate to 100 Hz, right?

That is correct. The nengo.dists.Choice distribution randomly uniformly chooses values from the given list. Since the given list has only 1 item (100), all of the neurons in the network are initialized to have a “maximum” firing rate of 100Hz. Note that this “maximum” is when the neuron is being presented with an input value of 1, and not the true maximum firing rate (which is $1/tau_{ref}$).

@Choozi

The intercept is the intercept for a neuron to start firing, am I right?

This is also correct. And in the code, since the intercepts are initialized to 0, neurons will only start firing when their input values exceeds 0.

@Choozi

Now coming to the main questions. Changing the amplitude of the neuron gives me the following accuracy plot.

Changing the amplitude of the neuron changes the amplitude of the spikes that are produced by the spiking LIF neuron model. Increasing the spike amplitude has the effect of increasing the amount of information being passed to subsequent neuron layers. Increasing the spike amplitude essentially scales the output of that neuron. I.e., if that neuron was outputting a “1”, doubling the spike amplitude would make it output a “2” (I’ll have to double check if the scaling is linear, but the sake of simplicity, it’s linear in this explanation).

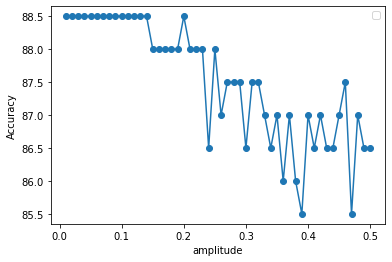
Increasing the spike amplitude itself wouldn’t cause too much of an issue if the network weights are trained to utilize these spike amplitudes. However, if have left do_training = False, then the network has been trained to use the smaller amplitudes, but is then being presented with the bigger spike amplitudes. Logically, this would impact the accuracy of the network, and cause a decrease in the overall accuracy, which is what you see here.

As for the zig-zag nature of the accuracy, this is because you are only looking at the accuracy results of one run of the network. Additionally, the network creation is seeded, so you’re basically running the same network over and over. Because the network is seeded, it could be that for some network amplitudes the network does okay (even if it wasn’t trained for it) just due to spike timings and filtering effects. But, if you increase or decrease the amplitude by a bit, those spike timings could arrive too close or too far apart causing a dip in accuracy.

If you want to get the overall trend of increasing the neuron amplitude, you’ll want to run the network multiple times using different seeds (you’ll need to train up the “base” network with a seed, then increase the amplitude for that seed).

[Choozi]

@xchoo Thank you for your answers.

Increasing the spike amplitude itself wouldn’t cause too much of an issue if the network weights are trained to utilize these spike amplitudes. However, if have left do_training = False , then the network has been trained to use the smaller amplitudes, but is then being presented with the bigger spike amplitudes. Logically, this would impact the accuracy of the network, and cause a decrease in the overall accuracy, which is what you see here.

For every amplitude value, I am creating a new network with seed = 0 and then train and test it. And the behavior is the same… with increasing the amplitude the accuracy drops down.
There is no more zig zag effect and this I do not understand why. First I was creating the network in a loop, but now I copied the network to a function and calling it from the loop.
So if the amplitude increase the amount of information passing to the subseqeunt neurons then if not increased atleast keep the accuracy more or less the same. But it is drop drastically. For every amplitude value I am keeping the seed=0.
So is this only because of the seed=0? as I am not using suitable seed for every amplitude. Or are there other parameters aswell?

[xchoo]

@Choozi

There is no more zig zag effect and this I do not understand why. First I was creating the network in a loop, but now I copied the network to a function and calling it from the loop.

This really depends on how you have coded it. If you are making the network in a function, you need to make sure the network is seeded inside the function. Otherwise, the network is seeded once, and the subsequent networks being created are not using the same seed. An easy way to test if your looped function is working is to keep the amplitude the same for every loop. In this case, the accuracy should not decrease at all.

@Choozi

So if the amplitude increase the amount of information passing to the subseqeunt neurons then if not increased atleast keep the accuracy more or less the same.

No. This would not be the case. Consider, for example, a very simple network with two layers, and that you have trained the network to just replicate the input (i.e., a communication channel):
$ input → layer1 → layer2 → output$
So, when you provide an input of 1, the output will be 1.
Now suppose you increase the amplitude of the neurons. For simplicity, let’s say we double the amplitude of the neurons, and let’s assume this has the effect of doubling the output of the layer. I.e., for an input of 1, the output will be 2. By any metric, the accuracy of the network has now decreased, even though “more information” is passing through the network.

@Choozi

So is this only because of the seed=0? as I am not using suitable seed for every amplitude. Or are there other parameters aswell?

Using a seed must be done carefully. In our examples we seed the network to ensure that the results demonstrated in the code is reproduceable. However, if you want to explore general trends in the network (i.e., what happens when you tweak parameters of the network), you’ll want to use other seeds as well. It could be that the network performs extremely well in one seed, but very poorly with another, and only by analyzing multiple seeds can you start to see the overall trend.

[Choozi]

@xchoo

This really depends on how you have coded it. If you are making the network in a function, you need to make sure the network is seeded inside the function. Otherwise, the network is seeded once, and the subsequent networks being created are not using the same seed. An easy way to test if your looped function is working is to keep the amplitude the same for every loop. I’n this case, the accuracy should not decrease at all.

Check it with the same amplitude value in a loop and the accuracy is not dropping.

@xchoo

No. This would not be the case. Consider, for example, a very simple network with two layers, and that you have trained the network to just replicate the input (i.e., a communication channel):
input → layer1 → layer2 → output
So, when you provide an input of 1, the output will be 1.
Now suppose you increase the amplitude of the neurons. For simplicity, let’s say we double the amplitude of the neurons, and let’s assume this has the effect of doubling the output of the layer. I.e., for an input of 1, the output will be 2. By any metric, the accuracy of the network has now decreased, even though “more information” is passing through the network.

Thank for the the explanation… it answered my question

@xchoo

Using a seed must be done carefully. In our examples we seed the network to ensure that the results demonstrated in the code is reproduceable. However, if you want to explore general trends in the network (i.e., what happens when you tweak parameters of the network), you’ll want to use other seeds as well. It could be that the network performs extremely well in one seed, but very poorly with another, and only by analyzing multiple seeds can you start to see the overall trend.

Alright! Thank you for the detailed answer.!