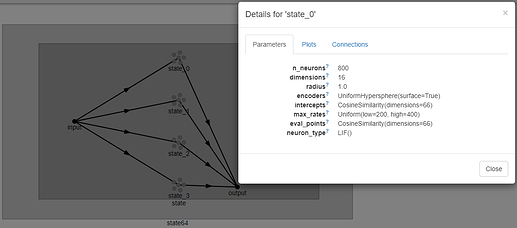
Hello @FilipD, and thank you for the most interesting question!
I must admit, I was quite stumped with this question myself. Initially, I had thought that the answer was simple: The saturation dynamics of an integrator in a higher dimensional space are different than that of a 1D integrator. As it turns out, my intuition about integrator dynamics was completely wrong (and it took some experimentation to figure this out), and this isn’t the actual answer, as I will demonstrate below.
First, to the claim that feeding in a regular-ol’ integrator would cause the output to saturate over time. I presume you mean that the output would “saturate” at a value above that of 1. From my experimentation, this is actually not the case. The code below creates two Nengo ensembles, both with the same neuron parameters. One ensemble is set up as a integrator, and the other is left in the feedforward configuration. The input to the integrator is a constant input of 1. The input to the “feed-forward” ensemble is a ramp that emulates the ramp output of an ideal (non-neural) integrator. Both ensembles use the LIFRate neuron type for smoother plots, but the findings generalize to spiking neurons as well.
Here’s the code:
import time
import nengo
import matplotlib.pyplot as plt
with nengo.Network() as model:
neuron_type = nengo.LIFRate()
nn = 50
radius = 1
seed = int(time.time())
print("Using seed: ", seed)
ramp_scale = 1
ramp = nengo.Node(lambda t: t * ramp_scale)
level = nengo.Node(ramp_scale)
ens_ens = nengo.Ensemble(nn, 1, seed=seed, neuron_type=neuron_type, radius=radius)
nengo.Connection(ramp, ens_ens)
tau = 0.1 # Feedback synapse for the integrator
int_ens = nengo.Ensemble(nn, 1, seed=seed, neuron_type=neuron_type, radius=radius)
nengo.Connection(level, int_ens, transform=tau, synapse=tau)
nengo.Connection(int_ens, int_ens, synapse=tau)
p_ramp = nengo.Probe(ramp)
p_ens = nengo.Probe(ens_ens, synapse=0.01)
p_int = nengo.Probe(int_ens, synapse=0.01)
with nengo.Simulator(model) as sim:
sim.run(3)
plt.figure()
plt.plot(sim.trange(), sim.data[p_ens], label="ens")
plt.plot(sim.trange(), sim.data[p_int], label="integrator")
plt.plot(sim.trange(), sim.data[p_ramp], 'k--', label="ramp")
plt.plot([0, 3], [radius, radius], 'r--')
plt.ylim(0, 2)
plt.legend()
plt.show()
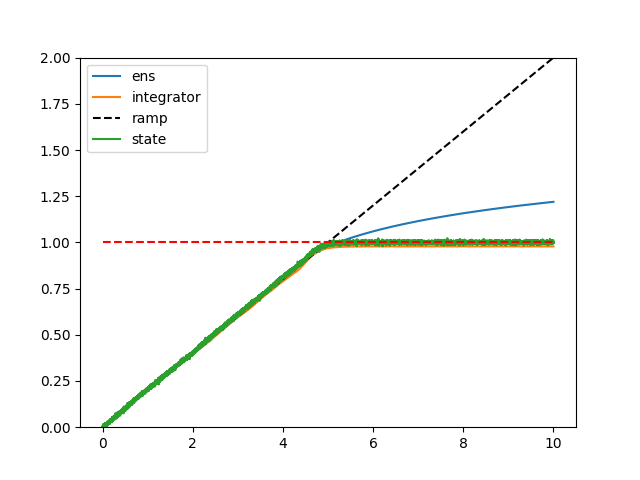
And here is the resulting plot!
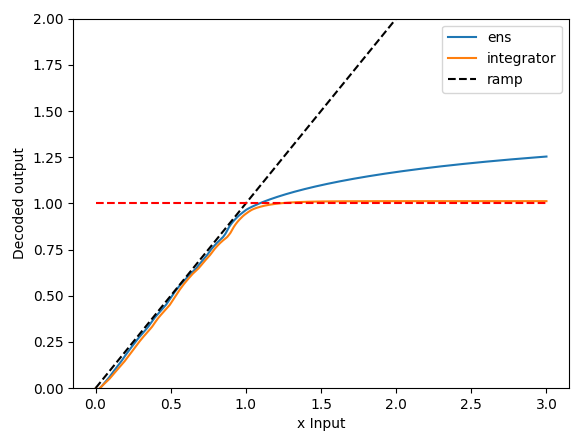
Let’s take a closer look at the plot, and make some observations:
- The output of the integrator and feed-forward ensemble both follow the ideal ramping behaviour quite closely. This means that the integrator is doing what it is meant to do (integrate a constant input to output a ramp), and so is the feed-forward ensemble (take the ramp into and output a ramp output).
- From $x=0$ to $x=1$, the feed-forward output follows the integrator output quite closely. We would expect this to be the case since both ensembles have been initialized with the same neuron parameters. It’s not 100% identical because the feed-forward ensemble doesn’t account for the feedback dynamics present in the integrator ensemble.
- Past $x=1$, the output of the feed-forward ensemble isn’t able to stick to the ramp ideal, but, this is to be expected as the ensemble is optimized in the range of $-1 < x < 1$, so everything outside that range is off the table.
- Also, as expected, when the feed-forward ensemble is driven with a large enough input, the output of the ensemble saturates (doesn’t keep increasing) because the neurons themselves are firing at their maximum rates.
- The output of the integrator “saturates” at about 1! Honestly, when I first saw this, I double checked my code thinking I had made a mistake. My original intuition was the saturation behaviour should reflect that of the feed-forward ensemble (which is clearly not the case here).
So… what is going on here? Why does the output of the integrator “saturate” at about 1? The output of the feed-forward ensemble in the plot above gives us a clue. You can think about an integrator as a bunch of fixed points, with the input to the integrator acting to push the value stored in the integrator from fixed point to fixed point. In an ideal integrator, the fixed points are infinitely close together. However, in the neural integrator, the fixed points are determined by crossing points where the neural output crosses the $y=x$ line. Coincidentally, the $y=x$ line is also the ramp input we provided to the feed-forward ensemble, so we can look at that output to deduce the behaviour of the integrator. And, if you look at the output, you’ll notice that about $x=0.92$, the output of the neural ensemble starts to diverge from the ideal $y=x$ line. What this means is that for any input greater than $x=0.92$, the integrator’s feedback value will be less than the input, stopping the integrator from integrating any further, and the value of the integrator falls back to the last fixed point (plus the input value) – which happens (for this seed) to be about 1 (0.92 + 0.1 [the input] ~= 1.02 [the observed value]). If you run the code multiple times, you’ll see that the “saturation” value of the integrator varies from run to run, sometimes below 1, sometimes above 1, but generally about 1.
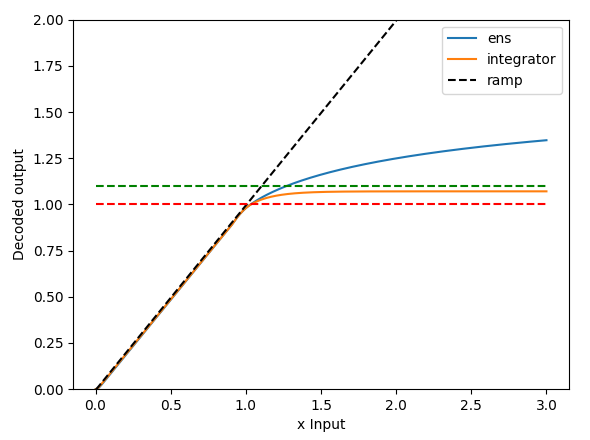
And you can experiment with the code as well. By increasing the number of neurons in the integrator to some super large number (the plot below uses 10000), the integrator becomes more ideal, so the last fixed point approaches $x=1, y=1$. In the graph below, the last fixed point is about 0.98, so with the input of about 0.1, the “saturated” integrator value is about 1.08 (the green dashed line represents 1.1)
Okay. So that’s the integrator “saturation” behaviour in 1 dimension. What about multiple dimensions? Well, this behaviour extends to multiple dimensions as well (which answers your original question).
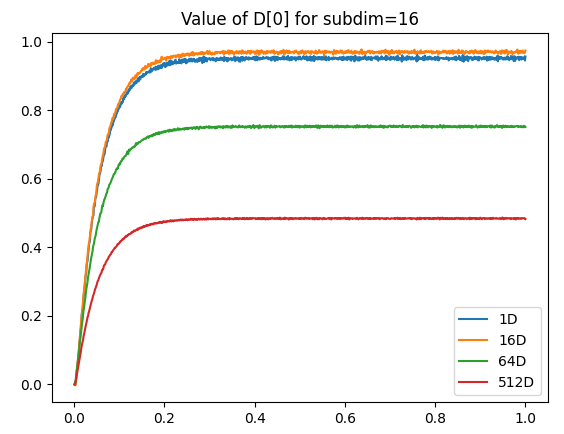
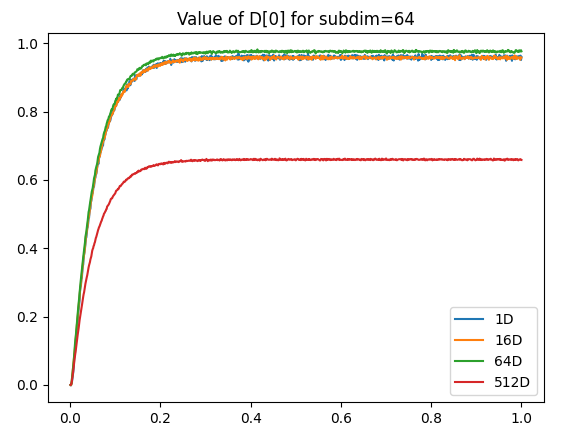
As a side note, I’m not 100% sure why, but as you increase the number of dimensions, the maximum “saturated” value represented by the integrator can actually increase as well. Below is a comparison of the vector norm of an output vector stored in several multi-dimensional integrators (1D, 8D, 16D). Each integrator is feed with a constant input of a vector projected along the x-axis.
Note: The plot below is a rather extreme example. The “saturation” value of the 8D and 16D generally ranges from about 1.1-1.3.
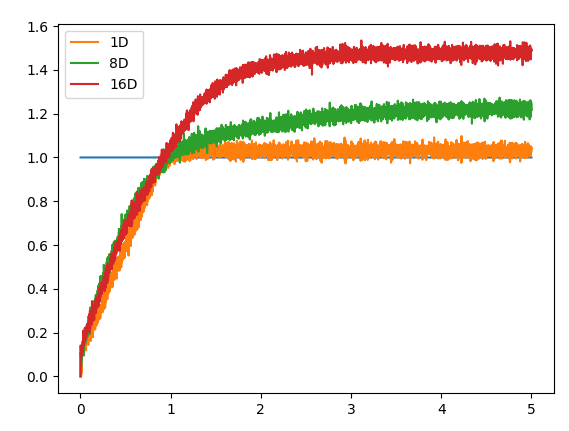
Here is the code:
import numpy as np
import nengo
import matplotlib.pyplot as plt
tau = 0.1
with nengo.Network() as model:
in_node = nengo.Node(lambda t: 1)
ens1 = nengo.Ensemble(50, 1)
ens2 = nengo.Ensemble(50 * 8, 8)
ens3 = nengo.Ensemble(50 * 16, 16)
nengo.Connection(in_node, ens1, transform=tau)
nengo.Connection(ens1, ens1, synapse=tau)
nengo.Connection(in_node, ens2[0], transform=tau)
nengo.Connection(ens2, ens2, synapse=tau)
nengo.Connection(in_node, ens3[0], transform=tau)
nengo.Connection(ens3, ens3, synapse=tau)
pi = nengo.Probe(in_node)
p1 = nengo.Probe(ens1, synapse=0.01)
p2 = nengo.Probe(ens2, synapse=0.01)
p3 = nengo.Probe(ens3, synapse=0.01)
with nengo.Simulator(model) as sim:
sim.run(5)
norm1 = np.linalg.norm(sim.data[p1], axis=1)
norm2 = np.linalg.norm(sim.data[p2], axis=1)
norm3 = np.linalg.norm(sim.data[p3], axis=1)
plt.figure()
plt.plot(sim.trange(), sim.data[pi])
plt.plot(sim.trange(), norm1, label="1D")
plt.plot(sim.trange(), norm2, label="8D")
plt.plot(sim.trange(), norm3, label="16D")
plt.legend()
plt.show()
I hope that helped! 






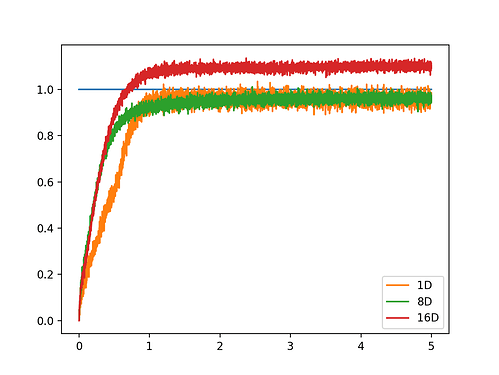

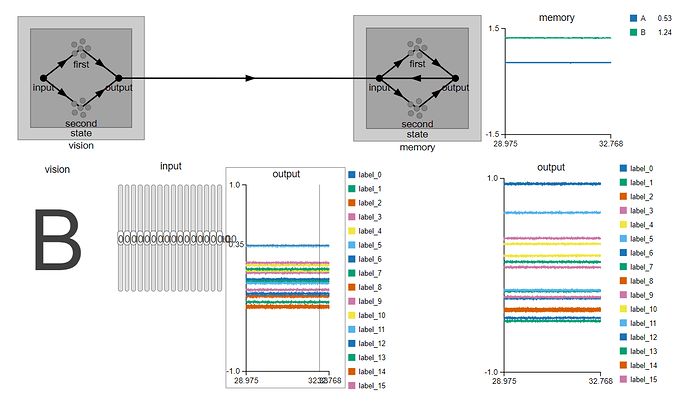
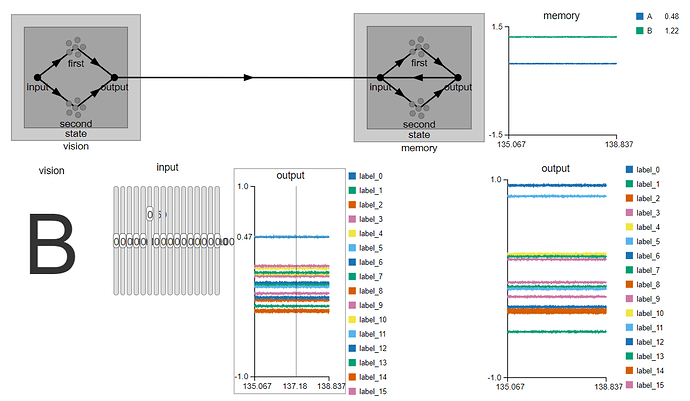
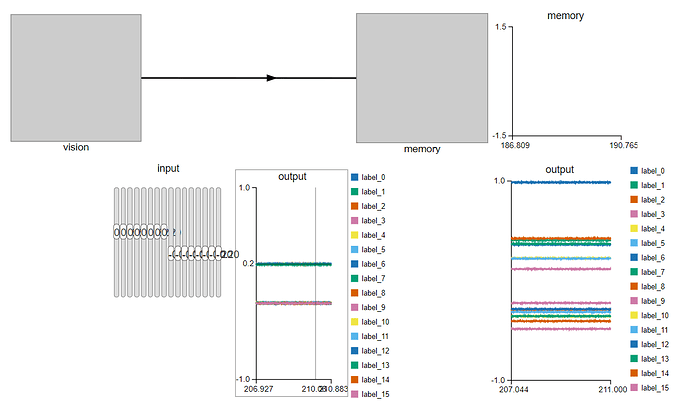
 . Is there any explanation for such behaviour in the implementation?
. Is there any explanation for such behaviour in the implementation?