MNIST value range for ensemble representation

[yedanqi]

Hi,

I am playing around with MNIST and trying to represent the (28,28) images as a nengo.Ensemble with dimensions of 784.

# Building the network
model = nengo.Network(label="MNIST")

with model:
    vision_input = nengo.Node(lambda t: preprocess(X_train[int(t)]), label="Visual Input")
    input_ensemble = nengo.Ensemble(
        n_neurons=n_neurons,
        dimensions=input_size
    )
    nengo.Connection(
        vision_input, input_ensemble
    )

    input_probe = nengo.Probe(vision_input, synapse=0.01)
    ens1_probe = nengo.Probe(input_ensemble)

It should be a simple network where input_ensemble just try to represent the original vision_input. However, input_ensemble can’t seem to represent this correctly (simulation ran for 5 seconds):

I have a hypothesis on what I could be doing wrong:
nengo.Ensemble default radius is 1, which I think is not correct since MNIST data range from 0 - 255. I tried changing radius to 255 which also yields the noisy image. I would like some advice on how to set the radius correctly, or perhaps I should normalize the MNIST data to unit vectors (or do some other preprocessing). I am using MNIST downloaded from tensorflow.keras.datasets.mnist as the nengo_extras dataset seems to be unreachable.

[yedanqi]

I made some improvements to this example and now it seems to be working better, though I feel the representation of the mnist digits can be further improved.

The few changes that I made that had a improvement include:

1. Since the pixels were fluctuating, I added a synapse=0.1 to the connection between input_ensemble and output.
2. Increasing the number of neurons from 1000 to 4000 helped in the overall representation power of the ensemble. This made the most improvements.
3. Increasing the radius of input_ensemble to 40, since the preprocessed MNIST pixel values still does not ensure that the image vector lies on a unit circle.

[xchoo]

Hi @yedanqi,

It seems like you have made some headway with this problem, but here are some additional tips to help improve the behaviour of your network.

@yedanqi

Since the pixels were fluctuating, I added a synapse=0.1 to the connection between input_ensemble and output.

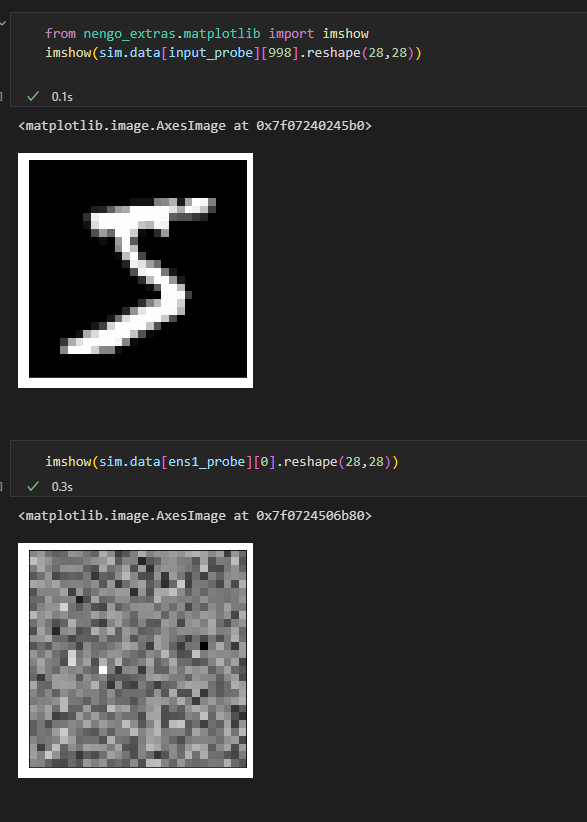
Right! In your Nengo, probes attached to objects do not have a synaptic filter applied to them by default. Thus, when you do this: ens1_probe = nengo.Probe(input_ensemble)
The ens1_probe is essentially recording the unfiltered (super spikey) output of the input_ensemble. To reduce the spikiness, you’ll need to add a synaptic filter (synapse) to the probe, as you did with input_probe. Note that in NengoGUI, any plots you display have a synaptic filter applied to them by default (I can’t recall what the exact value is… something like 0.01s?)

@yedanqi

Increasing the number of neurons from 1000 to 4000 helped in the overall representation power of the ensemble. This made the most improvements.

This is also the correct approach. If you think about the problem in a bit more depth, the input image (flattened as a vector) is 786-dimensional. With 1000 neurons in the ensemble, that’s sort of equivalent (not exactly equivalent, but a rough measure) to having each dimension being represented by 1.3 neurons. Considering that we typically use ~30 neurons to represent a 1D value, using just 1.3 neurons to do the same is… kinda pushing it.

I would recommend trying to use at least 30 neurons per dimension to represent the MNIST digit well, but then you run into another problem. At 30 neurons per dimension, the single input_ensemble ensemble would comprise 23,580 neurons… and it would take forever for Nengo to build that ensemble (because solving for the decoders is a scales with the number of neurons squared).

There are alternative approaches though. The easiest approach is to use an EnsembleArray (see this example too) to represent the MNIST digit. An ensemble array is basically a pre-built network containing a collection (array) of ensembles, where the input is split up (dimensionally) and sub-dimensions are represented by individual ensembles. With the default settings, the EnsembleArray is created such that 1 ensemble is used to represent each dimension of the input signal. While the number of neurons in the network remains the same (23,580), the advantage of the EnsembleArray is that building 786 30-neuron ensembles takes much much less time than one big 23,580 neuron ensemble.

The one caveat to using the EnsembleArray is that if you want to learn a function on all 786 dimensions of the MNIST input, you can’t do this with the EnsembleArray. Since each ensemble in the EnsembleArray represents each dimension (pixel) of the MNIST input independently, each ensemble does not have information about the other pixels, and thus constructing a function that involves those other pixels becomes impossible. The 2D equivalent of this problem would be trying to construct a network that does a product (i.e, A \times B) when each ensemble only knows about one of the inputs (either A or B, but not both together).

@yedanqi

Increasing the radius of input_ensemble to 40, since the preprocessed MNIST pixel values still does not ensure that the image vector lies on a unit circle.

Yup! This is another thing I would have suggested as well. Or rather, I would have suggested that you normalize the input images so that the overall (flattened) vector input is contained within the 768D hypersphere. Remember that when you feed a signal into a Nengo ensemble, that input is considered as a vector and each component of that input affects the magnitude of the vector. The radius of the Nengo ensemble must be optimized such that the expected magnitude of the input vector is within the radius of the ensemble. Note that the radius of the ensemble pertains to the whole vector, not just to individual vector components.

Consider the following procedure:

• You start with the MNIST image where each pixel is from 0-255.
• Next, you divide each pixel by 255 to get them into a range from 0-1.

What is the vector magnitude in this case? If we consider the extreme inputs, a solid white image (all 1’s) would have a vector magnitude of \sqrt{768} \approx 28 , which is much bigger than 1. This means that the ensemble will have a rough time trying to accurately represent the input signal.

There are several ways to address this issue. The quickest approach is to simply normalize each image in the dataset. This ensures that all of the input images have a vector magnitude of 1. However, this approach may lead to inconsistencies between images (images with more white pixels would look overall dimmer than images with less white pixels). You can also subtract the mean of all of the images in the dataset to remove any inherent bias (more or less white pixels) each image has. This is to make better use of the full representational range of the ensembles.

If you are intending to use the EnsembleArray to represent the MNIST signal, another thing to note is that each pixel takes on a value from 0-1, whereas each ensemble in the Ensemble Array can represent a 1D value from -1 to 1. This means that you are “wasting” half of your representational power, and you can make full use of it by biasing the pixel values so that they take on values from -1 to 1.

[yedanqi]

@xchoo, thanks! As always your replies are most helpful!

I tried out your suggestions above. First, I normalized the images to unit vectors using the following preprocessing function:

def preprocess(img):
    X = img.reshape(-1)
    X = X - np.mean(X)
    return X / np.linalg.norm(X)

This allowed me to tune the radius of the ensemble back to 1, but you were right about the images being very dimly lit. Here is a picture of what it looks like:

Next, I swapped the Ensemble with an EnsembleArray, making each ensemble represent 1 pixel/1 dimension:

input_ensemble = nengo.networks.EnsembleArray(
        n_neurons=30,
        n_ensembles=784,
        ens_dimensions=1
    )

The result is I got a much clearer picture:

I have no other questions on this for now as I will go back to my autoencoder problem but let me know if you spot anything I shouldn’t be doing.

[yedanqi]

Hi @xchoo, I would like to follow up with a question for this example: Is there a way I can export the model with the solved decoders so that I can reuse it somewhere else without Nengo trying to solve for it again?

[xchoo]

Hi @yedanqi,

Yup, this forum topic summarizes how to save and load the weights of a Nengo network (read the entire thread).

[yedanqi]

@xchoo, thanks for recommending the thread! That forum topic is exactly what I was looking for. I will give it a try myself soon.