I decided to split up my response into two posts to keep them fairly readable. In this post I’ll discuss the approach I took to create an SNN that computes the metrics on discrete values. First and foremost, I recommend watching through this playlist of videos to familiarize yourself with the NEF and Nengo. It’ll make understanding the methods I discuss in the post easier.
I’ll use the STD function for my discussion here. To start, let’s look at the formula for STD:
\sigma = \sqrt{\frac{\sum{(x_i - \mu)^2}}{N}}, where N is the number of samples, \mu is the mean of the sample data, x_i is the value of each sample point, and \sigma is the STD. From the formula, we see that we need to compute the mean, as well as a square and square root, and a summation.
Let us start from the inside, and work our way outwards. First, how do we compute \mu? Well, \mu is the sum of all of the data values, divided by the number of data values there are. Mathematically, we can write it as so: \frac{x_0}{N} + \frac{x_1}{N} + ...
We can compute this with a dot product where we take the data vector and dot product with a vector that looks like this: [\frac{1}{N}, \frac{1}{N}, \frac{1}{N}, ...]
Since we can compute it with a dot product (i.e., a matrix operation), the mean can thus be computed using the transform parameter in a Nengo connection:
with nengo.Network() as model:
inp = nengo.Node(data)
mean = nengo.Ensemble(100, 1)
nengo.Connection(inp, mean, transform=np.ones((1, N)) * 1.0 / N)
Next up, let’s compute (x_i - \mu). We need to do this for each of the data values, so there will be N values that we need to represent. Instead of using N ensembles, here we will use a handy pre-built Nengo network (an EnsembleArray) that will do the organizational work for us. Note that since \mu, and the subtraction are all linear transformations, we can do all of the computation using just the nengo.Connections.
with nengo.Network() as model:
inp = nengo.Node(data)
ens_array = nengo.networks.EnsembleArray(100, N)
nengo.Connection(inp, ens_array.input) # x_i
nengo.Connection(inp, ens_array.input,
transform=np.ones((N, N)) * -1.0 / N) # - mu
Now, let’s compute the square. The EnsembleArray has a handy add_output function that allows us to apply a function to the values represented by each ensemble in the EnsembleArray. I.e., if the input to the EnsembleArray is [x_0, x_1, x_2, ...], the added output would represent [func(x_0), func(x_1), func(x_2), ...].
with model:
ens_array.add_output("square", lambda x: x **2)
Next is \frac{\sum{x}}{N}. We have the value of each (x_i - \mu)^2, and now we need to sum them all up and divide by N. This is just another mean function, and we know how to implement this. Also, we know that we still need to compute a square root function, so to do this computation, we’ll project it into a Nengo ensemble. One thing we have to careful of is that a Nengo ensemble is optimized to represent values from -1 to 1. If the result of the second mean operation results in values outside of this range, we’ll need to modify the second ensemble’s radius to compensate.
with model:
ens_array.add_output("square", lambda x: x **2)
mean_of_sqr = nengo.Ensemble(200, 1, radius=1) # Change the radius if needed
nengo.Connection(ens_array.square, mean_of_sqr,
transform=np.ones((1, N)) * 1.0 / N) # Note: using the "square" output of ens_array
Lastly, we need to compute the square-root of the mean-of-the-squares. This can be done using the function parameter on a nengo.Connection. Note that the square root function produces invalid values for x<0. Thus, the function we provide to the Nengo connection has a conditional block to deal with this special case.
def sqrt_func(x):
if x < 0:
return 0
else:
return np.sqrt(x)
with model:
result = nengo.Node(size_in=1)
nengo.Connection(mean_of_sqr, result, function=sqrt_func)
And that should be it! 
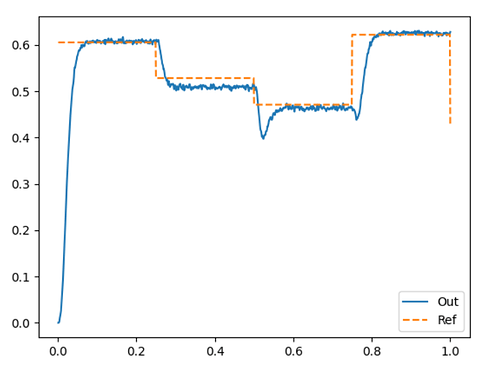
Here’s an example output of a network computing the STD on random 10-dimensional vectors:
Here’s the code I used to generate that figure:
test_nengo_std.py (1.5 KB)
You’ll notice that it does a reasonably good job computing the STD function, but it can at times be fairly incorrect. This is because the square root function is somewhat difficult to represent correctly, so you’ll need to play with the parameters of the mean_of_sqr ensemble. Here’s a test square root network you can use to do this:
test_nengo_sqrt.py (755 Bytes)
I should note that none of this code involves PES learning at all, and you must decide how you want to incorporate learning into these networks. With PES learning, you need to generate an error signal, which in turn requires a “reference” value (i.e., something that computes the function perfectly already), and I’m not quite sure how you want to do this. This Nengo example demonstrates this point.