I am currently looking at the Lorenz Attractor and I am curious to why I get this peculiar result.
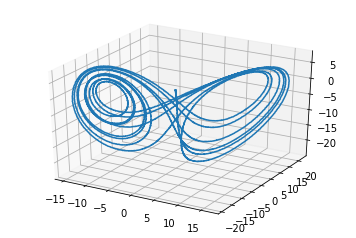
So first of all my understanding is that by using: sigma = 10, rho = 28, and sigma = 8/3 this system of equations gives us the butterfly chaotic attractor.
So we can consistently recreate the same attractor lets add a seed of 9 to the ensemble.
When we run the tutorial as it is with 2000 neurons we get a butterfly attractor.
If we reduce it to 500 we can still get a butterfly attractor.
However if we increase it to 1000 neurons we get a fixed point attractor and if we go to 4000 neurons we get a another fixed point attractor.
Why does an increase in neurons create a worse/wrong representation of the butterfly attractor?
1 Like
Try averaging the number of successes across a seed given a number of neurons.
Alternatively, you might want to compare how closely each attractor is following the ideal butterfly path, if possible.
I’m not that familiar with approximating dynamic systems, so I’m hoping someone will correct my attempt at a response.
1 Like
The idea of calculating successes is good and for the moment is what I’m rolling with.
The ideal butterfly path inst really something I believe we can measure (easily) due to the shape of a chaotic attractor being heavily reliant on initial conditions.
You can try also playing with the radius. The value of 60 may be a bit high, which means the tuning curves will be biased to approximate the function better in the wrong places. With 1000 neurons, and seed=9, which didn’t work for you, adjusting it to radius=30 fixes the problem.
Adding these two lines to the end:
import numpy as np
print(np.max(np.linalg.norm(sim.data[state_probe], axis=1)))
gives 27.2371789407 as the “actual” radius for ${\mathbf x}(t)$ from this simulation.
2 Likes
I also just wanted to point out, that although the difference between 60 and 30 may not seem like much, keep in mind these values refer to the radius of a 3-dimensional sphere (representing the state-space ${\mathbf x}(t)$), and the volume of such a sphere is $\mathcal{O}(r^3)$. Thus, a two-fold increase in $r$ translates to an eight-fold increase in volume, 7/8’ths of which are wasted trying to approximate this function in some unused domain. Therefore, the quality of the function approximation will depend on things such as how many evaluation points fall into the 1/8’th that is needed, and the dynamic range of the neurons across this same space. This also explains why it is seed-dependent.
1 Like
Thanks a million! Great explanations.
