LIF neuron bias and gain calculation

Examples & Tutorials
1

Hi,

I’m looking at the tutorial of NEF algorithm (https://www.nengo.ai/nengo/examples/advanced/nef-algorithm.html) and also playing with the intercepts.

I can understand and also derive how the gain and bias are obtained in generate_gain_and_bias function:

def generate_gain_and_bias(count, intercept_low, intercept_high, rate_low, rate_high):
    gain = []
    bias = []
    for i in range(count):
        intercept = random.uniform(intercept_low, intercept_high)
        z = 1.0 / (1 - math.exp((t_ref - (1.0 / rate)) / t_rc))
        g = (1 - z) / (intercept - 1.0)
        b = 1 - g * intercept
        gain.append(g)
        bias.append(b)
    return gain, bias

I slightly modified the above function in order to get evenly distributed intercepts, so it becomes:

def generate_gain_and_bias(count, intercept_low, intercept_high, rate_low, rate_high):
    gain = []
    bias = []
    ##################### my modification #####################
    intercepts = numpy.linspace(intercept_low, intercept_high, count)
    for i in range(count):
    ##################### my modification #####################
        intercept = intercepts[i]
        z = 1.0 / (1 - math.exp((t_ref - (1.0 / rate)) / t_rc))
        g = (1 - z) / (intercept - 1.0)
        b = 1 - g * intercept
        gain.append(g)
        bias.append(b)
    return gain, bias

However, the actual tuning is shown below. The intercepts are not evenly distributed. Though it looks more ‘even’ than the original version (the uniform distributed intercept).

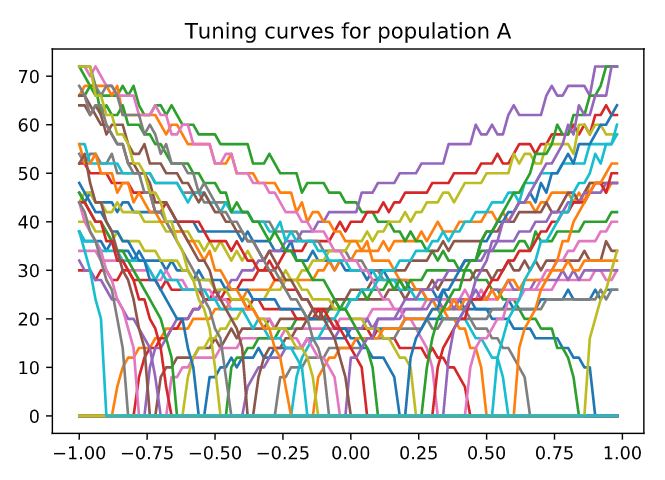
tuning_curve

In addition, there may be a bug, just right below the step 2 section

v_A = [0.0] * N_A  # voltage for population A
ref_A = [0.0] * N_A  # refractory period for population A
input_A = [0.0] * N_A  # input for population A

The refractory period of A and B are set to 0, but when calculate gain and bias, t_ref = 0.002 are used. First I suspect this may cause the mismatch between the desired and actual intercept. I change ```
ref_A and ref_B to 0.002, but it doesn’t fix the problem. desired and actual intercept still mismatch.

Then I checked how the intercept of LIF neuron is calculated in nengo source code. but the function is not implemented, so I guess nengo.neurons.NeuronType.gain_bias will be called to obtain the gain and bias. This function does not calculate gain and bias analytically, it looks like monte carlo method.

So my question is:
I believe the analytical solution (shown in first code block) to calculate gain and bias of LIF neuron is correct. But the actual result mismatches with my expectation, thet actual intercepts are not really evenly distributed. So I don’t know what’s going wrong.

My result should be quite easy to reproduce. The only relevant modification is shown in the second block. You can also set ref_A and ref_B to 0.002 instead of 0, but this doesn’t affect the tuning curve visibly.

2

Keep in mind that the intercepts are independent of the encoders. So you are starting with evenly distributed intercepts, and then (effectively) randomly flipping some of them to the left or right, which makes it look like they are not evenly distributed when you plot them. But if you remove the encoder flipping, for example by setting

encoder_A = [1 for i in range(N_A)]
encoder_B = [-1 for i in range(N_B)]

you can see that your intercepts are in fact evenly distributed.

That code section is setting up the variables that track the remaining time in the current refractory period of the neurons. At the beginning of the simulation none of the neurons have spiked yet, so their refractory time is all zero. The t_ref parameter is the time that is added to each of those variables whenever a neuron spikes, which you can see happening in the run_neurons function up above (ref[i] = t_ref).

LIF is a subclass of LIFRate, which implements the gain_bias method (analytically) here nengo/nengo/neurons.py at main · nengo/nengo · GitHub.

3

Thanks for quick response. Now I get correct result.