Now, I want to simulate the activation of LIF neuron on Nengo? I don’t know how I can do on Nengo. Can do anyone help me, please?
I’m not entirely sure what you are asking here. Nengo in itself simulates the activity of all of the neurons in a network. By default, the neurons are spiking LIF neurons. You can probe the spiking activity by probing the .neurons object:
p_spike = nengo.Probe(ens.neurons)
The Nengo documentation also provides several examples of demonstrating the activity of neurons. Refer to the single neuron example for reference code on how to do this.
Hi @xchoo
Thanks for your response. I am not sure but I know that synapse is used to filter the signals so I think it will discrete like spikes instead being continuous as the figure shows. So can you explain for me?
And I mean the activation of integration fire neuron on nengo
Sorry if I bother you @xchoo, but I don’t understand why are these equations in LIF class such as delta_t, voltage….? Can you explain for me or has any document about LIF so I can understand clearly about it? Thanks for your interest!
When you filter the spikes with a synaptic filter, it “smooths out” the spikes, resulting in a continuous signal, rather than discrete spikes. In Nengo, the synapse parameter simulate the postsynaptic potential (or postsynaptic current) generated by a spike arriving at a synapse.
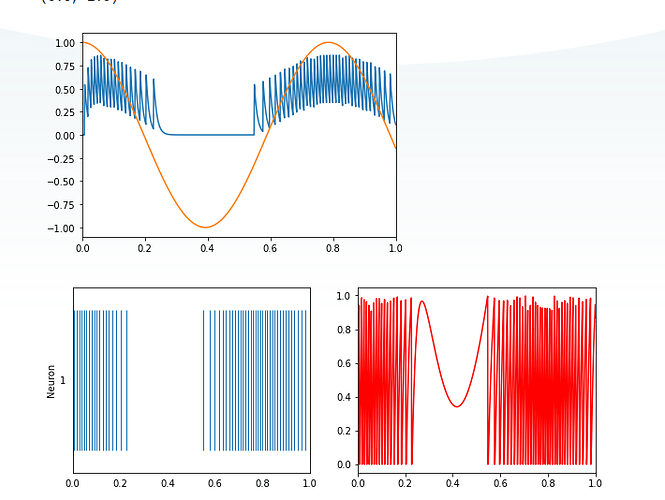
As for the plots, the details for each plot is described in the code. Namely, the top graph shows the “decoded” output (i.e., the spikes filtered by a synapse). The bottom left plot is the plot of the spike train (i.e., the individual spikes generated by the single neuron), and the bottom right plot is the plot of the membrane voltage of that single neuron.
I am still unsure what you mean by “activation of integration fire neuron”. If you are asking about the spike train of the neuron, that is described in the Nengo example I linked to in my previous post. If, however, you are asking about the mapping between the neuron’s input current and the neuron’s steady state firing rate (i.e., the neuron response curve), this Nengo example demonstrates how to generate that plot.
The step function you are referencing deals with how to update the neuron membrane voltage depending on the input current. The derivation of the voltage update code is essentially an implementation of the generic LIF neuron equations. An example of this derivation can be found in the Neural Engineering book, but other neuroscience literature should have this derivation (or similar forms of this derivation) as well.
In particular, the complication in Nengo’s implementation of the LIF equations attempts to rectify the issue of inaccuracies when dealing with discrete timesteps. In a naive implementation, where events only happen on the timestep boundaries, the simulated firing rate of a neuron can differ from the actual firing rate because refractory period resets don’t line up with the timestep boundaries. As an example, the delta_t code fixes this by using a fractional timestep.
Details on the changes to this part of the code base can be read with this git commit message.
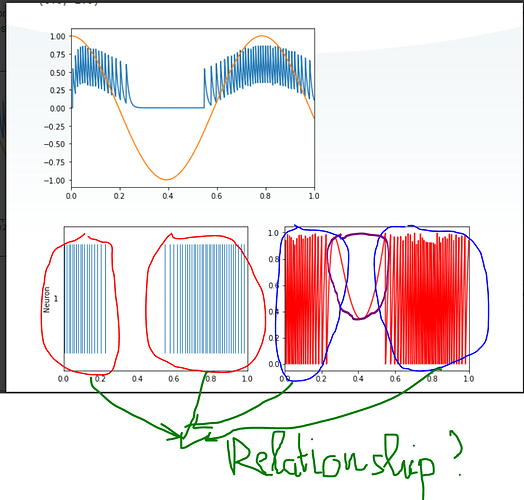
Thanks for your enthusiasm. Nevertheless, I am not clear about the plot of the spike train that the red line (I draw) is when a spike is fired, alright? Also, what is the relationship between the red and blue lines? They are quite the same. Moreover, what does a purple line mean?
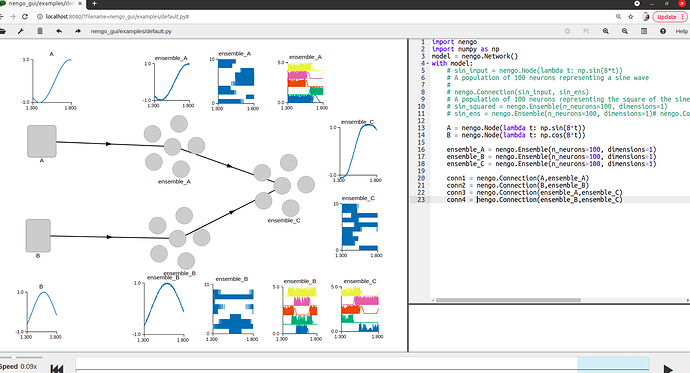
Also, I don’t know exactly how do the neurons of the ensemble connect? I read the source code Connection.py but I don’t see the code that reveals how are the neurons connected? Furthermore, I simulate the connection on Nengo GUI. When the input signal is a sin wave, if there is a neuron, the output signal is not clearly a sin signal . In contrast to, if there are 100 neurons, the output signal is a sin wave. So can you explain this phenomenon to me? Of course, I also bother the output spike when it has a neuron or 100 neurons. Maybe the more and more neurons, the output value is accurate more and more. The top picture is when it is a neuron and vice versa.
@xchoo ,
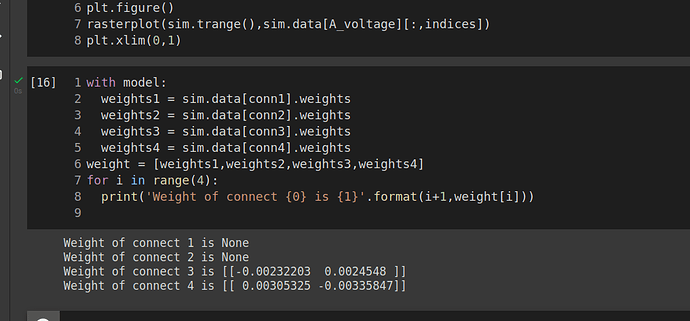
Sorry for bothering you. According to my knowledge, The output of a decoded connection is the sum of the pre ensemble’s neural activity weighted by the decoding weights solved for in the build process. However, when I print conn1.weights as well as conn2.weights are None so I wonder how the decoded output is calculated? Furthermore, I am not clear why conn1, conn2 weights are None, but conn3,conn4 are vice versa. As the result, If I don’t connect A input and ensemble_A, how the decoded output of ensemble_A is counted?
I have some documentation and simulated it on nengo GUI.
You can check this powerpoint link.
The lines circled in red are the individual spikes emitted from the neuron. That is correct.
The plot circled in blue is the plot of the neuron’s membrane voltage. When the membrane voltage exceeds a certain level (in this case, 1), a spike is emitted from the neuron. That is why the two plots are correlated.
That plot is the neuron membrane voltage. In that period of time, there is no input to the neuron (see the orange line in the top plot), which means that there is no input current into the neuron. Since the neuron is an LIF neuron (i.e., leaky), with no current input, the membrane voltage slowly decreases. As the input comes backup, input current is fed into the neuron, and the membrane voltage rises again.
This behaviour is a result of the NEF (neural engineering framework). This Youtube video series describes the NEF is detail and the second video (at about the 1hr 50min mark) describe how using more neurons will result in a better representation of the input signal.
In Nengo, if you create a connection without any weights (i.e., without using the function or transform parameters), Nengo will create a connection with the default weight of None. Internally, when Nengo sees this, it will build the connection and solve for decoders to approximate the identity function (i.e., the ensemble output will approximate the ensemble input).
To obtain the solved weights (i.e., the weights used when the simulation is running), you can probe for it using:
conn = nengo.Connection(...)
p_weights = nengo.Probe(conn, "weights", ...)
If you use the Nengo probe, it is advisable to set the sample_every parameter to reduce the amount of RAM your simulation uses (see an example here).
You can also obtain the solved weights by using this code:
with nengo.Simulator(model) as sim:
weights = sim.model.params[conn].weights
As a note, nengo.Node objects do not have decoder weights.
The decoders of an ensemble are solved to approximate a given function (see the NEF lectures). As part of the solving process, a bunch of evaluation points are internally generated by Nengo and used to solve for the decoders. This means that an ensemble can have decoded weights even without an input connection.
In your network, if you don’t connection the A node to ensemble_A, then the output of ensemble_A will just be 0.
I am glad to your response and I understand your point, but I mean why conn1, conn2 weights are None, but conn3,conn4 are vice versa while I don’t use the ‘function’ or ‘transform’ with 4 connections.
I don’t understand the question you are asking here… When I create the network as you have, all four connections have weights that are None (when you probe them using sim.model.params[connX].weights).
Can you provide some code regarding your question? Maybe show how you are obtaining and printing out the weights?
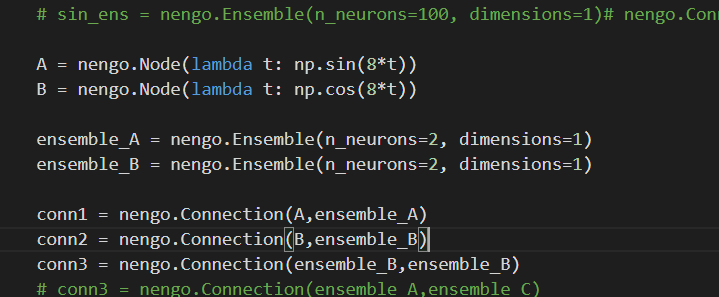
Really ??? because when I create the network, conn1 and conn2 weights are None but conn3 and conn4 aren’t too ( I edit n_neurons to 2 instead of 100)
also, I want to ask you a question about connection neurons in an ensemble. I read a paper written Nengo and that said neurons in the ensemble are connected by weight but I am not sure it is true? So can you tell me the answer?
Ah. I found a bug in the network I was implementing. You are correct in the observation that the weights for conn1 and conn2 are None, while conn3 and conn4 are some value. However, my original statement is still correct:
The .weights attribute returns the decoder weights for connections to / from ensembles, and the full connection matrix for connection from .neurons objects (e.g., ens.neurons). In your model conn1 and conn2 are connections from Nengo nodes, and thus they do not have decoder weights. Thus, the returned value is None. For nengo.Nodes, a None weight is treated as not changing the value the node is outputting.
If you create an ensemble on its own, and create a connection to it, e.g.:
with nengo.Network() as model:
ens_B = nengo.Ensemble(10, 1)
nengo.Connection(ens_A, ens_B)
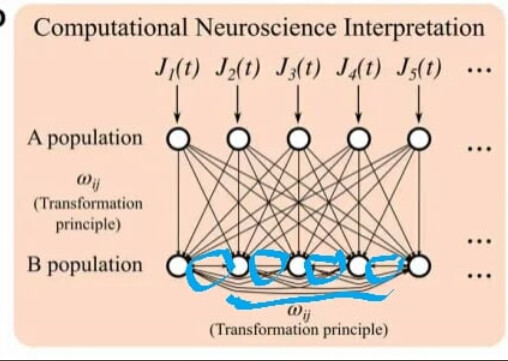
then no, there will be no weights between the neurons in the ens_B population. To achieve a network similar to what you have in the image, you’ll need to create a recurrent connection on the ens_B population:
with nengo.Network() as model:
ens_B = nengo.Ensemble(10, 1)
nengo.Connection(ens_A, ens_B)
nengo.Connection(ens_B, ens_B) # Recurrent connection
Yepp. Thank you so much, I understand what you said. Also, I wonder when an ensemble has many neurons( i.e 5 neurons) so when a spike is fired, how does the Nengo know it regarding what spike?
Yepp. I see however I wonder when I create a recurrent connection on the ens_B ( n_neurons = 2), the connection matrix has shape (1,4) due to each neuron in the ensemble will connect each other but the real matrix’s shape is (1,2)
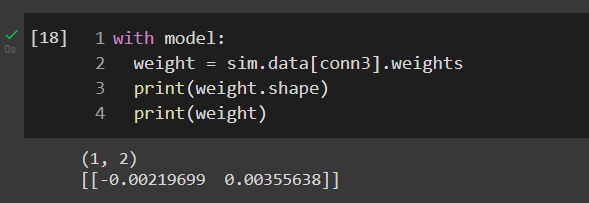
In Nengo, when you are connecting an ensemble to another ensemble (even if the destination ensemble is the same as the origin ensemble), the connection weights are always the decoders. In this case, ensemble_B has 2 neurons and is 1D, so the decoders will be a 2x1 matrix (note, depending on which way you set up your matrix convention, it can also be 1x2).
When connecting two ensembles, the weight matrices look like this:
input -> encoders -> ensemble -> decoders -> encoders -> ensemble -> decoders -> output
If the connection is a recurrent one, it would look something like this:
,-----------------------------,
V |
input -> encoders -> ensemble -> decoders -'
Note that if you connect directly to the neurons (using the .neurons attribute), you should get a 2x2 matrix. I don’t think there will be any instance where you will get a 1x4 connection matrix.
I am not sure what you mean?