Kanerva's "Dollar of Mexico" analogy in SPA

[simondlevy]

For the final assignment in my current neural nets class, I’m asking the students to implement Kanerva’s Dollar of Mexico analogy example in nengo_spa. I’ve attached the relevant section of the article as a screenshot.

Although we got it working with Gayler’s Multiply-Add-Permute flavor of binding, I’m having trouble getting good results using the nengo_spa code below. Any pro tips?

import matplotlib.pyplot as plt
import nengo
import nengo_spa as spa
import numpy as np

d = 32

with spa.Network() as model:

    # Maybe this will help?
    model.config[spa.State].neurons_per_dimension = 200

    fum =  spa.Transcode('(NAM*USA + CAP*WDC + MON*DOL) * (NAM*MEX + CAP*MXC + MON*PES)', output_vocab=d)

    query = spa.Transcode('DOL', output_vocab=d)

    result = spa.State(vocab=d)

    fum * ~query >> result

    p = nengo.Probe(result.output, synapse=0.01)

with nengo.Simulator(model) as sim:

    sim.run(0.5)

plt.plot(sim.trange(), spa.similarity(sim.data[p], result.vocab))
plt.xlabel("Time [s]")
plt.ylabel("Similarity")
plt.legend(result.vocab, loc='best')
plt.show()

[arvoelke]

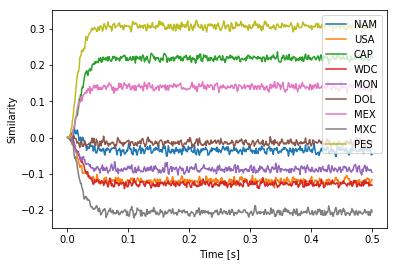
I believe the fundamental issue is the above vector algebra assumes that each vector is its own inverse (i.e., v == ~v, or v * v == 1, where 1 is the identity vector).

For example, when considering:

$$\begin{align}
F_{UM} &= \text{USTATES} \ast \text{MEXICO} \\
&= \left[ (\text{NAM} \ast \text{USA}) + (\text{CAP} \ast \text{WDC}) + (\text{MON} \ast \text{DOL}) \right] \ast \left[ (\text{NAM} \ast \text{MEX}) + (\text{CAP} \ast \text{MXC}) + (\text{MON} \ast \text{PES}) \right] \\
&\overset{?}{=} \left[ (\text{USA} \ast \text{MEX}) + (\text{WDC} \ast \text{MXC}) + (\text{DOL} \ast \text{PES}) + \text{noise} \right]
\end{align}$$

the question of equality depends on whether $(\text{NAM} \ast \text{USA}) \ast (\text{NAM} \ast \text{MEX}) \overset{?}{=} \text{USA} \ast \text{MEX}$, which relies on $\text{NAM}$ cancelling themselves to give the identity vector – and the same thing for the other two cases with $\text{CAP}$ and $\text{MON}$ cancelling themselves.

However, very few vectors in the HRR algebra are their own inverses. In fact, there are only $2^d$ such vectors. These are the vectors where each Fourier coefficient is either $-1$ or $1$ (such that each complex number either rotates itself to become the identity 1, or stays at 1, respectively).

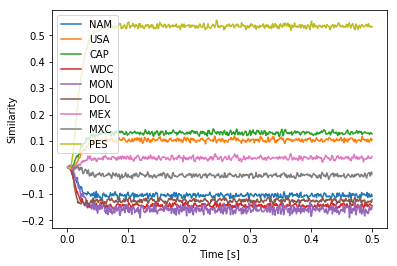
One work-around is to construct the query vector a little differently to fit the example and the HRR algebra. In particular, if we instead construct the query as DOL * MON * MON then its inverse will take care of the two MON that were bound together in $F_{UM}$. With 64 dimensions, this seems to work okay most of the time.

d = 64

with spa.Network(seed=0) as model:

    # Maybe this will help?
    model.config[spa.State].neurons_per_dimension = 200

    fum =  spa.Transcode('(NAM*USA + CAP*WDC + MON*DOL) * '
                         '(NAM*MEX + CAP*MXC + MON*PES)', output_vocab=d)

    query = spa.Transcode('DOL * MON * MON', output_vocab=d)

    result = spa.State(vocab=d)

    fum * ~query >> result

    p = nengo.Probe(result.output, synapse=0.01)

with nengo.Simulator(model) as sim:

    sim.run(0.5)

plt.plot(sim.trange(), spa.similarity(sim.data[p], result.vocab))
plt.xlabel("Time [s]")
plt.ylabel("Similarity")
plt.legend(result.vocab, loc='best')
plt.show()

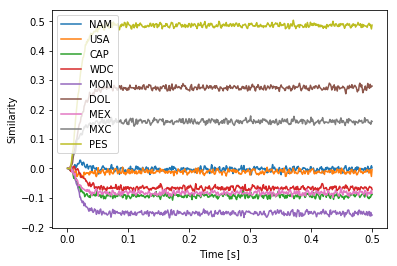
Another possibility is to pick a vector for MON that is its own inverse, i.e., satisfying MON = ~MON or equivalently MON * MON = 1, where 1 is the identity vector. Again, there are $2^d$ such vectors. To keep things simple, let’s just pick MON = -1. This also seems to work well most of the time.

vocab = spa.Vocabulary(
    dimensions=64, pointer_gen=np.random.RandomState(seed=0))

# Add the vectors in the same order as before
# to get consistent colours / legend
vocab.populate('NAM; USA; CAP; WDC')
vocab.add('MON', vocab.parse('-1'))
vocab.populate('DOL; MEX; MXC; PES')

# Check that it is its own inverse
assert np.allclose(vocab.parse('MON').v,
                   vocab.parse('~MON').v)

# Check that it cancels out to give the identity
assert np.allclose(vocab.parse('MON * MON').v,
                   vocab.parse('1').v)

with spa.Network(seed=0) as model:
    model.config[spa.State].neurons_per_dimension = 200

    fum =  spa.Transcode('(NAM*USA + CAP*WDC + MON*DOL) * '
                         '(NAM*MEX + CAP*MXC + MON*PES)',
                         output_vocab=vocab)

    query = spa.Transcode('DOL', output_vocab=vocab)

    result = spa.State(vocab=vocab)

    fum * ~query >> result

    p = nengo.Probe(result.output, synapse=0.01)

with nengo.Simulator(model) as sim:

    sim.run(0.5)

plt.plot(sim.trange(), spa.similarity(sim.data[p], result.vocab))
plt.xlabel("Time [s]")
plt.ylabel("Similarity")
plt.legend(result.vocab, loc='best')
plt.show()

[arvoelke]

And here is one last example that shows off the extensibility of the SPA software. We can define a custom algebra that extends what it means to be unitary to involve the additional constraint of being its own inverse (see discussion above). Then picking MON to be unitary does the same trick as the second example above, but much more generally (it becomes easy to impose the same constraint on NAM and CAP if so desired).

import matplotlib.pyplot as plt
import nengo
import nengo_spa as spa
import numpy as np


class CustomAlgebra(spa.algebras.HrrAlgebra):

    def make_unitary(self, v):
        # This is a hack for generating custom vectors
        # that are unitary but with the additional constraint
        # that every Fourier coefficient has magnitude 1 or -1
        # so that v is its own inverse (v == ~v)
        
        d = len(v)
        fft_val = np.fft.fft(v)
        fft_real = fft_val.real
        
        # This is achieved by having each coefficient either
        # act with a 180 degree rotation or no rotation
        # Arbitrarily pick which coefficients do what
        # in order to get 2^d possibilities
        fcoefs = fft_real < 0
        fft_real[fcoefs] = -1
        fft_real[~fcoefs] = +1

        return np.fft.ifft(fft_real, n=d).real


vocab = spa.Vocabulary(
    dimensions=64, pointer_gen=np.random.RandomState(seed=0),
    algebra=CustomAlgebra())

# Add the vectors in the same order as before
# to get consistent colours / legend
vocab.populate('NAM; USA; CAP; WDC')
#vocab.add('MON', vocab.parse('-1'))
vocab.populate('MON.unitary()')
vocab.populate('DOL; MEX; MXC; PES')

# Check that it is its own inverse
assert np.allclose(vocab.parse('MON').v,
                   vocab.parse('~MON').v)

# Check that it cancels out to give the identity
assert np.allclose(vocab.parse('MON * MON').v,
                   vocab.parse('1').v)

with spa.Network(seed=0) as model:
    model.config[spa.State].neurons_per_dimension = 200

    fum =  spa.Transcode('(NAM*USA + CAP*WDC + MON*DOL) * '
                         '(NAM*MEX + CAP*MXC + MON*PES)',
                         output_vocab=vocab)

    query = spa.Transcode('DOL', output_vocab=vocab)

    result = spa.State(vocab=vocab)

    fum * ~query >> result

    p = nengo.Probe(result.output, synapse=0.01)

with nengo.Simulator(model) as sim:

    sim.run(0.5)

plt.plot(sim.trange(), spa.similarity(sim.data[p], result.vocab))
plt.xlabel("Time [s]")
plt.ylabel("Similarity")
plt.legend(result.vocab, loc='best')
plt.show()

[simondlevy]

Thanks for explaining this so thoroughly, Aaron. I should’ve appreciated that Kanerva’s solution relies on the self-canceling of vectors in the overall construction, not just in the query phase. This will make the exercise even more of challenge to the students: a nice bonus!