Hi everyone,
I am just new to nengo and want to implement a full adder module in nengo. I have tried to implement the sum function using XOR operator “^” but the output goes only to almost .70 for 1 and 0.25 when the output should be 0. Is there any other way to implement the full adder module? However, the carry part works as intended. Also using a threshold function to get the logical values for 0 and 1.
Any form of suggestions is welcome.
thank you
Hai
Update
Now the XOR part works well instead of using the “^”, I have used the mathematical expression s=(a-b)(a-b) and for the carry function used carry=(s-c)(s-c). Is there any other efficent way to do this?.
Thanks
Hi @SubinSam, and welcome to the Nengo forums! 
Your request is an atypical one. The spiking neural networks implemented in Nengo are generally more well suited to functions with continuous outputs, since the function approximation done by the NEF algorithm rely partly on the smoothing operation (i.e., smoothing a spike train into an “average” continuous value) done by the synapses of the neural connections. Since the various signals moving about the neural network are smoothed, it is very difficult (but not impossible) to get exact 0’s and 1’s that are typical of binary operators.
That said, it is still possible to use various tricks in Nengo (and the NEF) to get a neural ensemble to approximate the function of a full adder. I will elaborate on these tricks below!
Setting Evaluation Points
When you create a nengo.Ensemble, by default, Nengo will optimize the input and output weights of that ensemble to try and represent a value anywhere within the unit (having a radius of 1) hypersphere (sphere / circle of arbitrary dimensions). For scalar values, this means Nengo will try to make the ensemble the best* (*relative to things outside the unit hypersphere) for values within the range of -1 to 1.
For your problem in particular, since you are only dealing with a binary representation, a lot of the representational optimization is “wasted” since the ensemble has been optimized for the range of -1 to 1, while the inputs are either 0 or 1. (If you have questions about why the representational optimization is “wasted”, let me know, and I’ll try to explain it in more detail in a follow up reply)
Nengo, however, allows you to adjust what input values to use for the optimization process, to “focus” the optimization at those specific values. To do this, set the eval_points argument when creating an ensemble. The example that follows creates a 2-dimensional ensemble that is optimized to represent the four possible combinations of 2-input binary values:
ens = nengo.Ensemble(
100,
2,
eval_points=nengo.dists.Choice([[0, 0], [0, 1], [1, 0], [1, 1]])
)
Note 1: The nengo.dists.Choice is a built-in Nengo distribution function that samples from a list of vectors. By using the Choice distribution in this way, Nengo is being instructed to generate optimization evaluation points only from the provided list of vectors, and this “focuses” the optimization on just these values.
Note 2: There are smarter ways of generating all of the possible combinations of binary values for $N$ inputs, but I’ll leave that up to you to fill in.
Defining Custom Output Functions
You probably have experience defining custom output functions (at least it seems so from your first post), so the advice here pertains to this question of yours:
One of the advantages of using Nengo is that by using the NEF algorithm, Nengo can create spiking neural ensembles that can implement any function. Nengo achieves this by using the NEF algorithm to solve for output weights such that combined with the response curves of the neurons, the neural ensemble approximates a mapping between a set of input values and a set of desired output values (where the output values lie along the function to be implemented).
Note: The caveat to the “an ensemble can implement any function” is that the ensemble isn’t really implementing the function per se, just doing an approximation of the function.
I’m not sure what your exact implementation of the full adder module is, but the statement I made above means that you can create an “efficient” implementation by making the full adder circuit in one ensemble, rather than by using one ensemble to implement each of the basic binary gates that make up the full adder. I’ll start you off with some code below, and let you experiment in finishing it:
def full_adder_func(x):
a, b, cin = map(int, x) # Split up the x input into their respective parts, and convert to binary values
# Implement full adder logic here
sum = ...
cout = ...
# Return the sum and carry out as a 2-dimensional vector
return [sum, cout]
with nengo.Network() as model:
# Define a 3-dimensional ensemble. Three dimensions are needed to represent
# all of the inputs to the full-adder (A, B, CarryIn)
ens = nengo.Ensemble(100, 3, eval_points=...)
# Output of the full adder has 2 values, here we are just using a node
# so we have something to connect to.
out = nengo.Node(size_in=2)
# Create the nengo connection that "implements" the full adder function
nengo.Connection(ens, out, function=full_adder_func)
Results
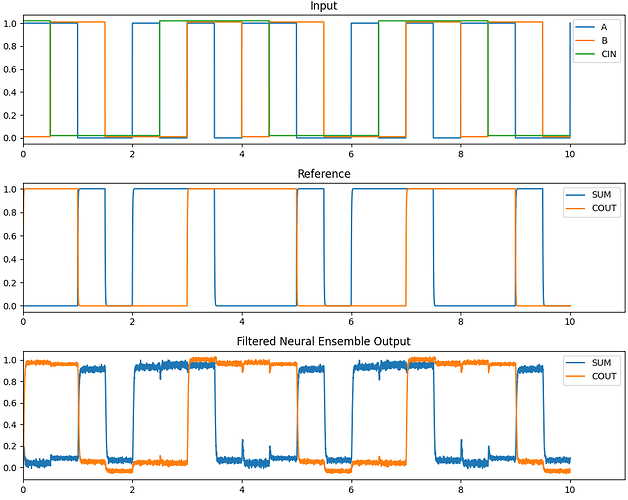
Just as a bit of a teaser, I did write my own implementation of the full adder module with all of the points I addressed above. With my implementation these were the results!
Note 1: I did not implement an additional thresholding circuit in my implementation, it is just one neural ensemble.
Note 2: In the “Input” plot, I manually offset the A, B, and CIN lines so that each line is more distinct on the plot. Otherwise, they would have overlapped each other and it was difficult to see what the actual values were. The inputs to the network are, however, binary (i.e., not offset).
Thanks a lot of the detailed explanation. I have learned a lot. If I am understanding it right the function “Choice” allows you to define an area rather than a circle by default for optimization.
What is the best way to give input to ensemble? Is it Piecewise function or is there any other efficient way to do it?
Not quite. The NEF optimization process maps a set of input points (in vector space – with a dimensionality equals to the dimensionality of the ensemble that is being optimized), to a set of output points (the output dimensionality is defined by the output function that you want the ensemble to represent). By default, Nengo chooses a set of input points such that it is uniformly distributed within the unit hypersphere. However, by using the Choice distribution, you are overriding this default, and telling Nengo to only use the input points defined by the Choice distribution.
There is no “best” way to feed inputs to an ensemble. Any method (e.g., defining your own function and using a Node) will work. However, if you are looking to implement piecewise function, I’d recommend checking out the built-in nengo.processes.Piecewise process.
