Hi,
I would like to create the following If logic into ensemble C
I have 2 neuron ensembles A and B that each encodes a value that can range from -1 to 1.
C = { A, abs(B)>th
0, otherwise
what is the simplest way to implement this logic with nengo?
Thanks!
Hi @hadarcd, and welcome back to the Nengo forums. 
The cool thing about Nengo is that it has the NEF algorithm built into it to create neural networks to approximate any function, even the complex one you want to implement. The simplest way to implement the logic is to use the function parameter on a nengo.Connection. Here’s how you would do it:
First, we make the observation that the function you want to implement is a function of 2 variables, A and B. This means that to approximate this function, we’ll need to create a nengo.Ensemble of 2-dimensions, to be able to represent both A and B together at the same time. Also, since both A and B can range from -1 to 1, we’ll need this 2D ensemble to be able to represent [1, 1] (i.e., it needs a radius of \sqrt{2}. All of these steps are similar to Nengo’s multiplication example, which would make sense, seeing as a multiplication is also a function of 2 variables.
So, here’s what we have so far:
with nengo.Network() as model:
ensA = nengo.Ensemble(50, 1) # Represents A on its own
ensB = nengo.Ensemble(50, 1) # Represents B on its own
ensC = nengo.Ensemble(200, 2, radius=np.sqrt(2)) # Represents the combined [A, B] vector
nengo.Connection(ensA, ensC[0]) # Project the value of A to the first dimension of ensC
nengo.Connection(ensB, ensC[1]) # Project the value of B to the second dimension of ensC
With the 2D ensemble, we can now provide Nengo with a function to approximate when computing the decoding weights on ensC. This is where we will use the function you want to implement:
with model:
def logic_func(x): # Define the output function
a, b = x # Extract out the values for A and B
if b > thresh:
return a
else:
return 0
out = nengo.Node(size_in=1) # Create an output node
nengo.Connection(ensC, out, function=logic_func)
And that’s basically it! Here’s some test code you can run:
import matplotlib.pyplot as plt
import nengo
import numpy as np
thresh = 0.5
with nengo.Network() as model:
inpA = nengo.Node(lambda t: np.sin(t * 3 * np.pi))
inpB = nengo.Node(lambda t: t - 1.5)
out = nengo.Node(size_in=1)
ensA = nengo.Ensemble(50, 1)
ensB = nengo.Ensemble(50, 1)
ensC = nengo.Ensemble(200, 2, radius=np.sqrt(2))
nengo.Connection(inpA, ensA)
nengo.Connection(inpB, ensB)
nengo.Connection(ensA, ensC[0])
nengo.Connection(ensB, ensC[1])
def logic_func(x):
a, b = x
if abs(b) > thresh:
return a
else:
return 0
nengo.Connection(ensC, out, function=logic_func)
p_ina = nengo.Probe(inpA)
p_inb = nengo.Probe(inpB)
p_out = nengo.Probe(out, synapse=0.005)
with nengo.Simulator(model) as sim:
sim.run(3)
plt.figure()
plt.plot(sim.trange(), sim.data[p_ina])
plt.plot(sim.trange(), sim.data[p_inb])
plt.plot(sim.trange(), sim.data[p_out])
plt.plot([0, 3, 0, 0, 3], [thresh, thresh, None, -thresh, -thresh], "--")
If you run the code, you’ll see that it does a semi-reasonable job of approximating the logic function you specified, although it does have some difficulty when B is near the threshold value. But this is to be expected since that represents a discontinuity in the function, and it’s hard to approximate the sharp discontinuity (it’ll probably do better if you increase the number of neurons in ensC). This is an example plot:
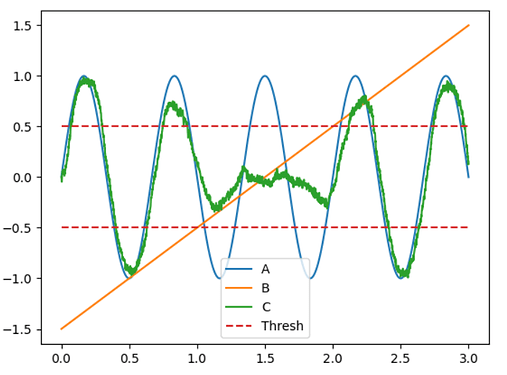
I didn’t want to make the previous post overly long, so here’s a follow up post!
The code I posted in the previous post is the “simple” first-pass implementation of the logic function but as you have observed, near the discontinuity, the approximated function breaks down quite a bit because of the decoder’s inability to approximate such a sharp function. However, with a slightly more advanced knowledge of Nengo, one can build a more faithful implementation of the function you specified.
If you examine the function you want to represent, part of the function specifies that the output should be 0 if a certain condition is met. In Nengo, one can use inhibitory gating to quiet (set to 0) the output of any neural ensemble regardless of the input it is being provided, thus all that is required to implement the desired function is to inhibit the output of C when the threshold conditions of B are not met.
Doing this, however, is a little complex. The first step is to figure out what the inhibitory signal needs to be given the value of B. From the logic formulation, the output of C should be 0 if abs(B) \leq threshold. Since the inhibitory signal needs to have a non-zero value when the inhibition is desired, we need to create a network that will output a non-zero value when abs(B) \leq threshold. Creating an ensemble that outputs a value (e.g., 1) only when the input is above a certain threshold is not too difficult. Here we can take advantage of the neuron encoders and intercepts to achieve this:
with nengo.Network() as model:
inhib = nengo.Ensemble(
50, 1,
intercepts=nengo.dists.Uniform(0, 0.1),
encoders=nengo.dists.Choice([[1]]),
)
inhib_out = nengo.Node(size_in=1)
nengo.Connection(inhib , inhib_out, function=lambda x: 1)
In the code above, the ensemble is configured such that all of the encoders are in the positive direction. This ensures that all of the neurons in the ensemble respond in a similar manner w.r.t to the sign of the input (i.e., no neurons will be active when x=-1, and all neurons will be active when x=1). Next, the intercepts are set be between [0, 0.1). This means that the neurons in the ensemble will only be active when the input to the ensemble (x) is greater than 0. Since we are not concerned with the output, and only that it has to be a non-zero value, we squish the intercepts of the neurons to be in the small range to maximum the representation of the sharp discontinuity at the threshold value. Finally, we apply an output function of lambda x: 1 to ensure that when the ensemble is active, some non-zero output is produced.
The threshold ensemble above only implements the function inhib\_out= 1 \text{ if } x \geq 0. To implement the function inhib = 1 \text{ if } abs(B) \leq threshold, we need another ensemble. This ensemble will represent the value of B, and approximate the function abs(B):
with model:
ensB = nengo.Ensemble(30, 1)
nengo.Connection(ensB, inhib, function=lambda x: -abs(x) + thresh)
In the code above, we do a little bit of math to connect the value of ensemble B to the inhibitory threshold ensemble. Since the inhibitory threshold ensemble is active when it’s input is \geq 0, if we provide it the input value of -abs(B) + thresh, this will ensure that for all values of B < thresh, the input to the inhibitory ensemble will be \leq 0, and for all values of B > thresh, the input to the inhibitory ensemble will be \geq 0, as desired.
Next, we’ll need to construct the rest of the network. This part is relatively straightforward. Looking at the desired logic function, C = A when it is not 0. Thus, we’ll need an ensemble to “pass through” the value of A to the output C:
with model:
ensA = nengo.Ensemble(30, 1)
ensC = nengo.Ensemble(30, 1)
nengo.Connection(ensA, ensC)
Finally, to have this “pass through” ensemble output 0 when desired, we just need to do the inhibitory connection:
with model:
nengo.Connection(inhib_out, ensC.neurons, transform=[[-20]] * ensC.n_neurons)
In the code above, we put a large weight on the inhibitory transform just to ensure that the inhibition takes place even if the output of inhib_out is weak.
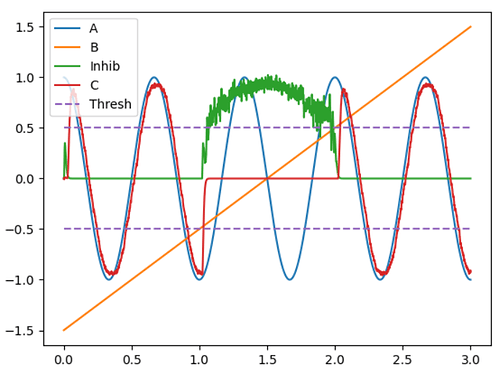
Putting all of this code together, we get this:
import matplotlib.pyplot as plt
import nengo
import numpy as np
thresh = 0.5
with nengo.Network() as model2:
inpA = nengo.Node(lambda t: np.cos(t * 3 * np.pi))
inpB = nengo.Node(lambda t: t - 1.5)
out = nengo.Node(size_in=1)
inhibout = nengo.Node(size_in=1)
ensA = nengo.Ensemble(30, 1)
ensB = nengo.Ensemble(30, 1)
inhib = nengo.Ensemble(
50,
1,
intercepts=nengo.dists.Uniform(0, 0.1),
encoders=nengo.dists.Choice([[1]]),
)
ensC = nengo.Ensemble(30, 1)
nengo.Connection(inpA, ensA)
nengo.Connection(inpB, ensB)
nengo.Connection(ensB, inhib, function=lambda x: -abs(x) + thresh)
nengo.Connection(ensA, ensC)
nengo.Connection(
inhib, ensC.neurons, transform=[[-20]] * ensC.n_neurons, function=lambda x: 1
)
nengo.Connection(inhib, inhibout, function=lambda x: 1)
nengo.Connection(ensC, out)
p_ina = nengo.Probe(inpA)
p_inb = nengo.Probe(inpB)
p_inh = nengo.Probe(inhibout, synapse=0.005)
p_out = nengo.Probe(out, synapse=0.005)
with nengo.Simulator(model2) as sim2:
sim2.run(3)
plt.figure()
plt.plot(sim2.trange(), sim2.data[p_ina])
plt.plot(sim2.trange(), sim2.data[p_inb])
plt.plot(sim2.trange(), sim2.data[p_inh])
plt.plot(sim2.trange(), sim2.data[p_out])
plt.plot([0, 3, 0, 0, 3], [thresh, thresh, None, -thresh, -thresh], "--")
plt.legend(["A", "B", "Inhib", "C", "Thresh"])
plt.show()
Note that in the code above, the inhibout node isn’t really necessary since I’ve put the function=lambda x: 1 configuration in the connection from inhib to ensC.neurons.
And this produces this output, which is more faithful to the original function.
You can play around with the number of neurons in the inhibitory ensemble, the intercept values (currently 0 to 0.1), the inhibitory weight (currently at -20), and the inhibitory connection synapse (currently default) to get different responses to the inhibition. I recommend doing some exploration.
