Hi,everyone!
I am trying to build a bionic network. How to realize the excitatory and inhibitory connection between neurons?
I have tried to set it like this:
weights = np.ones((B.n_neurons, A.n_neurons))
conn_demo=nengo.Connection(A.neurons,B.neurons,transform=weights)
The weights are all set to 1, I think the B neuron will completely convey the A neuron’s signal. But this is not the case.
Where did I get it wrong? How should the excitatory and inhibitory connections between neurons be expressed? I would be very grateful if you can answer my question.
Hello @YL0910, I am not sure how much will I be able to help you but thought to let you know of nengo-bio which supports explicit excitatory and inhibitory connections. Here is the GitHub link and the repo is maintained by @astoecke. I haven’t used it at all. With nengo I have used explicit negative weights to symbolize inhibitory connections.
BTW, you might want to check your last sentence in your question! 
Oh… I’m sorry for such a mistake. Thank you for your answer! I have tried using nengo-bio, but it doesn’t seem to be able to use nengo-dl.
With nengo I have used explicit negative weights to symbolize inhibitory connections.
How to set negative weights? If possible, can you provide some examples for me to learn from? Thank you very much!
Hi! Perhaps I can help you with your questions:
====================
I am trying to build a bionic network. How to realize the excitatory and inhibitory connection between neurons?
This really depends on specific constraints in the excitatory & inhibitory connection implementation. If your primary concern is with building a network that transfers information from population A’s neurons to population B’s neurons without wanting to worry about setting up the individual excitatory and inhibitory connections, then Nengo already does this for you.
pop_A = nengo.Ensemble(n_neurons=10, dimensions=1)
pop_B = nengo.Ensemble(n_neurons=20, dimensions=1)
nengo.Connection(pop_A, pop_B)
And that’s it! With the code above, Nengo will create a connection between population A and B and solve for the appropriate connection weights in order to perform the x=y function. Note that in the code above, the connection weights that Nengo solves for you contains a mix excitatory and inhibitory connections.
If you are looking to create a network where the excitatory and inhibitory connections are separate connections, you can use something like the nengo-bio codebase (as @zerone mentioned), or do what we refer to as the “Parisien” transform. This transform is used to convert a “standard” Nengo connection, where both inhibitory and excitatory connections can originate from the same neuron, into a network where inhibitory and excitatory connections are divided so that an individual neuron can either only be inhibitory or excitatory.
There is a fairly large github thread discussing it, with an example Nengo model defined here. Not that this uses the Dales solver from the parisien branch of the nengo-extras repository. The Parisien transform can also be done using nengo-bio with example code here.
I’m not entirely sure what your use case is, but you did mention NengoDL in your original query? If you are using NengoDL, some work will be needed to convert these example for use in NengoDL.
====================
The weights are all set to 1, I think the B neuron will completely convey the A neuron’s signal. But this is not the case.
What you are observing may be a result of a slight misunderstanding of what information Nengo is showing to you. When you do something like this:
pop_A = nengo.Ensemble(50, 1)
probe_A = nengo.Probe(pop_A, synapse=0.005)
what probe_A is probing is the decoded output of the ensemble pop_A. In order to get the decoded output of an ensemble, Nengo performs an optimization calculation to determine a set of output weights such that for a specific set of inputs (to the neural ensemble), the decoded output (i.e., the spike rate multiplied by the output weights) of the neural ensemble performs a specific function. By default, the function is an identity function (i.e., output = input). However, because Nengo generates neurons with randomly determined response curves, this often means that the output weights for any specific neural ensemble contain both positive and negative numbers. Going back to your question, where you specified a neurons-to-neurons connection weight of all 1’s, what this means is that your A population is indeed driving all the neurons in the B population, but because of the mix of positive and negative output weights, the decoded output averages out to 0. To see the effect of population A driving the neurons of population B, you’ll need to probe the spikes of the B population:
probe_spikes_B = nengo.Probe(pop_B.neurons)
====================
How to set negative weights? If possible, can you provide some examples for me to learn from? Thank you very much!
You’ve almost got it in the original example code you provided. Creating an inhibitory connection in Nengo works something like this:
pop_A = nengo.Ensemble(50, 1)
inhibitory_input = nengo.Node()
inhibitory_conn = nengo.Connection(inhibitory_input, pop_A.neurons,
transform=[[-1]] * pop_A.n_neurons)
If connecting from another neural ensemble:
pop_A = nengo.Ensemble(50, 1)
pop_B = nengo.Node()
inhibitory_conn = nengo.Connection(pop_B, pop_A.neurons,
transform=[[-1]] * pop_A.n_neurons)
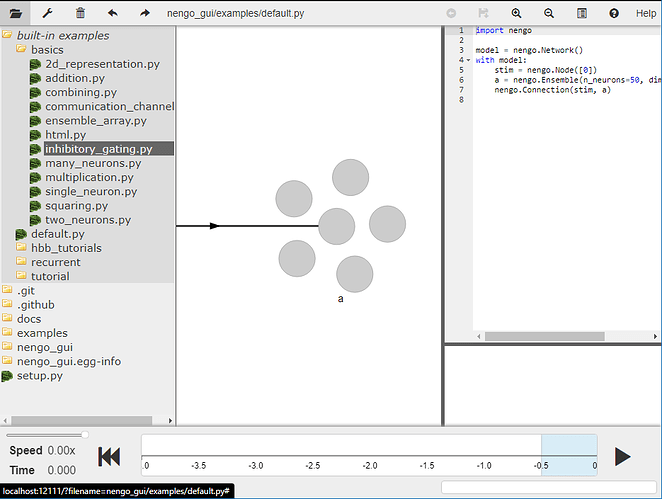
There is also an example of creating inhibitory connections in our NengoGUI. You can find it under “built-in examples” → “basics” → inhibitory_gating.py
If you don’t have NengoGUI installed, you can find instructions on how to do so here.
Thanks @xchoo for a very informative answer. @YL0910, the way I explicitly mentioned inhibitory connections between two neuron populations is as follows. It is similar to the way @xchoo has suggested.
Create a population:
model = nengo.Network(seed=7878)
with model:
ens_x = nengo.Ensemble(n_neurons=num_neurons, dimensions=dim,
intercepts=nengo.dists.CosineSimilarity(dim+2),
max_rates=nengo.dists.Uniform(50, 150),
seed=7879) # Seed value here is important.
conn = nengo.Connection(ens_x, ens_x, transform=A_p, synapse=tau)
Note that my use case was with recurrent connections, therefore I created one which computes a linear transform function which is denoted by the matrix A_p. Now we need the explicit weights of the neuron connections which we can obtain the following way:
with nengo.Simulator(model) as sim:
aTD = sim.data[conn].weights # This is alpha (gain of post population
# neurons), T, and D. T is transformation matrix.
E = sim.data[ens_x].encoders
W = E @ aTD
When you print the W matrix, you will find some positive entries and some negative entries. As the convention goes, positive entries are excitatory connections and negative entries are inhibitory connections. It’s equivalent to one neuron creating excitatory and inhibitory connections both, to other neurons. So you cannot consider this to be a network where a single neuron is either excitatory or inhibitory.
Once you obtain the W matrix you can create another model with explicit weights between ensemble neurons as follows:
model = nengo.Network(seed=7878)
with model:
ens_x = nengo.Ensemble(n_neurons=num_neurons, dimensions=dim, seed=7879,
max_rates=nengo.dists.Uniform(50, 150),
intercepts=nengo.dists.CosineSimilarity(dim+2))
nengo.Connection(ens_x.neurons, ens_x.neurons, transform=W, synapse=tau)
ens_output_probe = nengo.Probe(ens_x, synapse=10e-3)
Note that I am using the same seed values while creating the model and ensemble ens_x. Hope this helps.
Hi,xchoo!
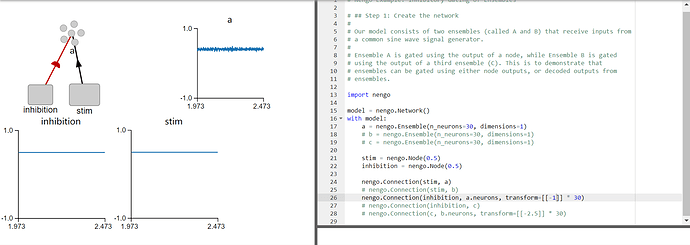
I am very happy to see such a detailed answer. By the way, I have studied the tutorial of neno-gui, as shown in the figure, why is the value of A ensembles not 0 when transform=-1?
The short answer is that you should set the value in the transform to something larger (e.g., [-5] instead of [-1]) to fully inhibit the ensemble in this example.
The longer answer has to do with the default tuning curves of the ensemble, and what they will cause the ensemble to do in the absence of any external input current. You can see that even if you don’t provide any stimulus or inhibition to the ensemble, as in:
with model:
a = nengo.Ensemble(n_neurons=30, dimensions=1)
(and nothing else) you will see approximately half of the neurons spiking. That is because the tuning curves are distributed by default to be uniformly tiled and randomly flipped across the range [-1, 1]. More specifically, each neuron has an associated bias term that can cause it to spike even in the absence of external current. This is beneficial in typical cases because it allows the ensemble to compute nonlinear functions across the interval [-1, 1] of represented values, but you can also change this behaviour by configuring the tuning curves of the ensemble (through the gain and bias, or equivalently the max_rates and intercepts). You can also right-click the ensemble in the GUI to display the tuning curves.
Some resources that may be helpful for more information:
To expand upon what @arvoelke posted specifically looking at the network you included in your post, the reason why the output of the A ensemble is not 0 when transform=-1 is as follows:
The stim value provided to the A ensemble is 0.5. The inhibition value provided to the A ensemble is also 0.5. This means that the total input (x) the ensemble can be determined by this formula (this is specific to your network):
x = stim + inhibition * inhibition_transform
In the case of the given values, this value is x = 0.5 + 0.5 * -1 = 0.
To get an idea of what the output of the ensemble A would look like for this input (x = 0), we’ll have to take a look at the neuron response curves. Here are some example neuron response curves (copied from the Nengo example @arvoelke posted)
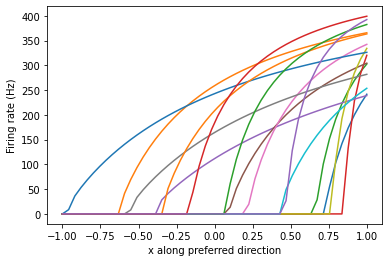
We can see from the response curves that for an input value of x = 0, some of the neurons are still active. This indicates that the ensemble is not fully inhibited and will produce an output (like you see in your network).
As a general rule of thumb, when designing Nengo networks with inhibition, you’ll want to make sure that:
(maximum_expected_ensemble_input +
minimum_inhibition_input_value * inhibition_transform) >= -1
or
inhibition_transform >=
(-1 - maximum_expected_ensemble_input) / minimum_inhibition_input_value
For your network in particular, the maximum_expected_ensemble_input = 1, and minimum_inhibition_input_value = 0.5. That means that in order to achieve a fully inhibitable ensemble, you should use an inhibition_transform of (-1 - 1) / 0.5 = -4.