In case this can help anyone, I’ve coded up this VirtualEnsemble helper network that scales to thousands of recurrently connected neurons. However, due to some other issues posted on GitHub I don’t yet have an example that shows off the benefits. A feed-forward example is at the bottom. I will make edits to this post as the network / applications are improved.
import numpy as np
import nengo
from nengo.params import IntParam
from nengo.utils.builder import default_n_eval_points
import nengo_loihi
from nengo_loihi.builder import get_gain_bias, get_samples
from nengo_loihi.neurons import loihi_rates
class VirtualEnsemble(nengo.Network):
"""Virtualize a single ensemble using multiple sub-ensembles.
The naming comes from an analogy to "virtual memory" in PCs.
Since Loihi maps each ensemble to one core, large ensembles with
dense connection matrices can easily consume all of the memory.
A solution is to partition the ensemble across multiple cores,
and then jointly optimize for decoders across all sub-ensembles.
This network achieves this by configuring the tuning curves
in advance and stacking the optimization problems together to
connect up each output pre-build time. This provides an
Ensemble-like interface, that can be connected into and decoded
from, but is implemented using multiple sub-ensembles underneath.
TODO:
- document and test
- add_output assumes function is a callable
- label the ensembles, node, connections
"""
n_ensembles = IntParam('n_ensembles', low=1)
def __init__(self, n_ensembles, n_neurons_per_ensemble,
intercept_limit=0.95, rng=np.random,
label=None, seed=None, add_to_container=None,
**ens_kwargs):
super(VirtualEnsemble, self).__init__(
label=label, seed=seed, add_to_container=add_to_container)
for illegal in ('eval_points', 'n_eval_points'):
if illegal in ens_kwargs:
raise ValueError("Ensemble parameter '%s' is unsupported" % illegal)
self._ensembles = []
self.n_ensembles = n_ensembles
self.n_neurons_per_ensemble = n_neurons_per_ensemble
with self:
for _ in range(n_ensembles):
ens = nengo.Ensemble(n_neurons=n_neurons_per_ensemble, **ens_kwargs)
gain, bias, max_rates, intercepts = get_gain_bias(
ens, rng=rng, intercept_limit=intercept_limit)
ens.gain = gain
ens.bias = bias
ens.max_rates = max_rates
ens.intercepts = intercepts
ens.encoders = get_samples(
ens.encoders, ens.n_neurons, ens.dimensions, rng=rng)
self._ensembles.append(ens)
# last ensemble is representative of all others in terms of dimensions
self.dimensions = ens.dimensions
def add_input(self, pre, weights=True, **conn_kwargs):
if weights:
transform = np.asarray(conn_kwargs.get('transform', 1))
with self:
for post in self._ensembles:
if weights:
conn_kwargs['transform'] = post.encoders.dot(transform)
post = post.neurons
nengo.Connection(pre, post, **conn_kwargs)
def add_neuron_output(self):
with self:
output = nengo.Node(size_in=self.n_neurons_per_ensemble * self.n_ensembles)
for i, ens in enumerate(self._ensembles):
nengo.Connection(ens.neurons, output[i*ens.n_neurons:(i+1)*ens.n_neurons],
synapse=None)
return output
def add_output(self,
function=lambda x: x,
eval_points=nengo.dists.UniformHypersphere(surface=False),
solver=nengo.solvers.LstsqL2(),
dt=0.001,
rng=np.random):
if not isinstance(eval_points, nengo.dists.Distribution):
raise TypeError("eval_points (%r) must be a "
"nengo.dists.Distribution" % eval_points)
n = self.n_ensembles * self.n_neurons_per_ensemble
n_points = default_n_eval_points(n, self.dimensions)
eval_points = eval_points.sample(n_points, self.dimensions, rng=rng)
A = np.empty((n_points, n))
Y = np.asarray([np.atleast_1d(function(ep)) for ep in eval_points])
size_out = Y.shape[1]
for i, ens in enumerate(self._ensembles):
x = np.dot(eval_points, ens.encoders.T / ens.radius)
activities = loihi_rates(ens.neuron_type, x, ens.gain, ens.bias, dt)
A[:, i*ens.n_neurons:(i+1)*ens.n_neurons] = activities
D, info = solver(A, Y, rng=rng) # AD ~ Y
assert D.shape == (n, size_out)
with self:
output = nengo.Node(size_in=size_out)
for i, ens in enumerate(self._ensembles):
# NoSolver work-around for Neurons -> Ensemble
# https://github.com/nengo/nengo-loihi/issues/152
# nengo.Connection(
# ens, output, synapse=None,
# solver=nengo.solvers.NoSolver(
# D[i*ens.n_neurons:(i+1)*ens.n_neurons, :],
# weights=False))
# TODO: investigate weird behaviour having something to do
# with the function not being respected when the
# add_output weights are embedded in NoSolver to form
# a recurrent passthrough
nengo.Connection(
ens.neurons, output, synapse=None,
transform=D[i*ens.n_neurons:(i+1)*ens.n_neurons, :].T)
return output, info
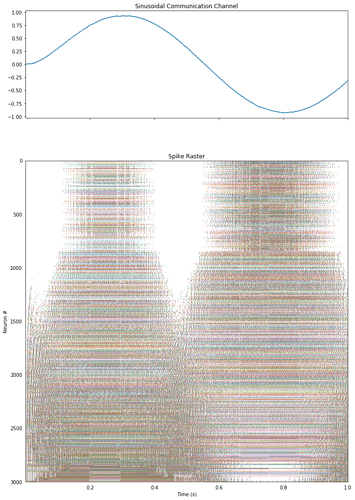
import matplotlib.pyplot as plt
import seaborn as sns
from nengo.utils.matplotlib import rasterplot
with nengo.Network() as model:
u = nengo.Node(output=lambda t: np.sin(2*np.pi*t))
x = VirtualEnsemble(
n_ensembles=30, n_neurons_per_ensemble=100, dimensions=1)
x.add_input(u, synapse=None)
x_hat, info = x.add_output()
p_x = nengo.Probe(x_hat, synapse=0.05)
p_a = nengo.Probe(x.add_neuron_output(), synapse=None)
with nengo_loihi.Simulator(model) as sim:
sim.run(1.0)
print("Decoder solver info:", info)
fig, ax = plt.subplots(2, 1, sharex=True, figsize=(12, 18),
gridspec_kw={'height_ratios': [1, 3]})
ax[0].set_title("Sinusoidal Communication Channel")
ax[0].plot(sim.trange(), sim.data[p_x])
A = sim.data[p_a]
t_slice = (sim.trange() > 0.4) & (sim.trange() < 0.55)
I = np.argsort(np.sum(A[t_slice], axis=0))
ax[1].set_title("Spike Raster")
rasterplot(sim.trange(), A[:, I], ax=ax[1])
ax[1].set_ylabel("Neuron #")
ax[1].set_xlabel("Time (s)")
fig.show()
Decoder solver info: {'rmses': array([0.00066519]), 'time': 0.4871366024017334}