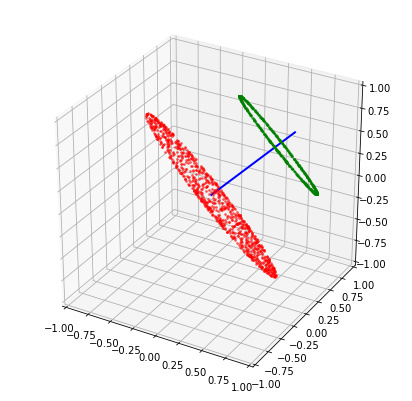
Ah! Well… it just so happens that you can also iterate the above procedure. In fact, this works out to be like an extended version of the Gram–Schmidt process! The trick is to maintain one matrix of orthogonalized vectors (via Gram–Schmidt), while simultaneously combining those vectors to build up the output matrix (via the above intuition). The challenge is to figure out the right scaling factors on these vectors in order to maintain the required invariant (by induction).
sphere = nengo.dists.UniformHypersphere(surface=True)
d = 6 # dimensionality
b = 0.8 # desired similarity
def proj(u, v):
return u.dot(v.T) / u.dot(u.T) * u
M = np.zeros((d, d)) # output matrix
Q = np.zeros((d, d)) # Gram-Schmidt orthogonalization of S
S = sphere.sample(d, d=d) # some random samples used to form Q
# Simultaneously apply Gram-Schmidt to S to compute Q while
# using Q to form M. This exploits the fact that
# Q[i, :].T.dot(M[j, :]) == 0 for all j < i.
for i in range(d):
Q[i, :] = S[i, :]
a = b/((i-1)*b + 1)
for j in range(i):
Q[i, :] -= proj(Q[j, :], S[i, :])
M[i, :] += a*M[j, :]
M[i, :] += np.sqrt((1 - i*a*b)/Q[i, :].T.dot(Q[i, :]))*Q[i, :]
print(M.dot(M.T))
[[ 1. 0.8 0.8 0.8 0.8 0.8]
[ 0.8 1. 0.8 0.8 0.8 0.8]
[ 0.8 0.8 1. 0.8 0.8 0.8]
[ 0.8 0.8 0.8 1. 0.8 0.8]
[ 0.8 0.8 0.8 0.8 1. 0.8]
[ 0.8 0.8 0.8 0.8 0.8 1. ]]
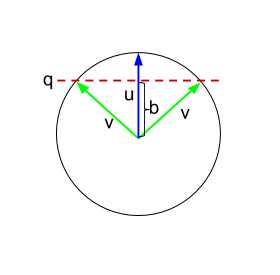
I would derive the magic scaling constants, but LaTeX is currently broken here. There’s also a lot that can be said regarding the geometry of the problem to motivate this way of combining the vectors, but, for the time being, I will leave this as an exercise for the reader. [Hints: By way of induction, write down all known dot-products using what you know about Gram–Schmidt as well as the fact that each vector in M is a linear combination of vectors from Q.]
In the end, this should be equivalent to Jan’s approach, but gives a geometrical perspective that may seem less mysterious to some. Understanding Jan’s approach also has value (he has a notebook with some details here and there is some very related discussion here). Note that both approaches only work for n <= d (essentially by the rank-nullity theorem).
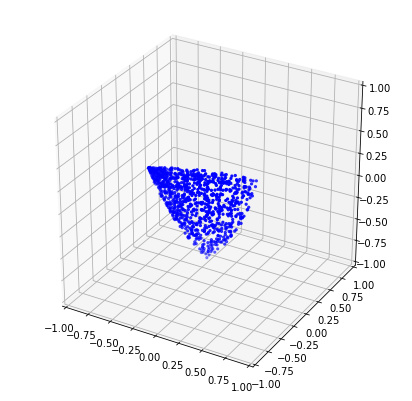
If we want n > d, then we require some sort of relaxation, for instance: bound the similarity below by some lower-bound. In this case, the d vectors of the matrix fully define the vertices of a convex surface from which to sample. More concretely, the surface is the set of all vectors on the sphere that have a dot-product of at least b with every vector in M. In this sense, the vectors in M act as “representatives” for the convex surface. Any two vectors drawn from this surface are guaranteed to have a similarity of at least b. Moreover, this surface has maximal area.
In three dimensions, this surface is an equilateral triangle covering the sphere. I haven’t tried thinking through a good way to uniformly sample this surface, apart from the obvious method of checking if random samples p satisfy np.all(M.dot(p.T) >= b) (see below).
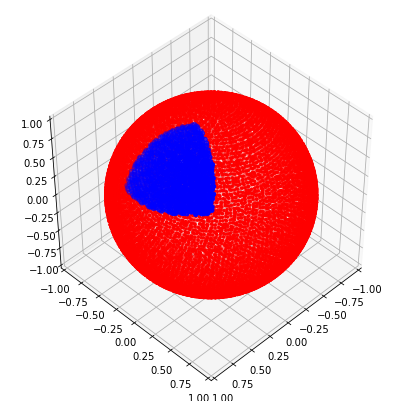
from nengolib.stats import sphere
from mpl_toolkits.mplot3d import Axes3D
good = []
bad = []
for p in sphere.sample(20000, d=d):
if np.all(M.dot(p.T) >= b):
good.append(p)
else:
bad.append(p)
good = np.asarray(good)
bad = np.asarray(bad)
assert np.all(good.dot(good.T) >= b)
plt.figure(figsize=(7, 7))
ax = plt.subplot(111, projection='3d')
ax.scatter(*bad.T, s=5, c='red')
ax.scatter(*good.T, s=20, c='blue')
#ax.scatter(*M.T, s=100, c='green')
ax.set_xlim3d(-1, 1)
ax.set_ylim3d(-1, 1)
ax.set_zlim3d(-1, 1)
ax.view_init(45, 45)
plt.show()
If you want to further restrict the dot-products to be no greater than some upper-bound, then things suddenly become much harder. In general, this reduces to the sphere-packing problem, which is an unsolved problem in mathematics. Only the solutions for a couple specific instances (e.g., the Leech lattice) are currently known. I would recommend randomly sampling, checking, and keeping/discarding (as done in the SPA).
One last thing worth mentioning: the above method assumes that the rows of S are linearly independent (in other words, they span the d-dimensional space). For uniformly and independently sampled vectors, this happens almost surely. However, with dependent sampling (e.g., nengolib.stats.sphere), this is no longer necessarily the case. So if you are experimenting with this, make sure that you are sampling/choosing S such that it can be orthogonalized, otherwise strange things may happen.