Encoders and stable dynamics for a Head Direction network

[MatthijsPals]

(See next post for quicker to answer questions that don’t need this context)

Dear all,

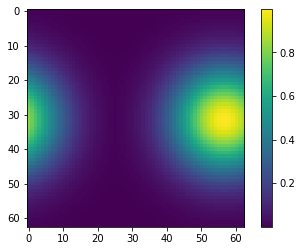
I am implementing a head direction network in Nengo, based on this publication: http://compneuro.uwaterloo.ca/files/publications/conklin.2005.pdf. In short, the neurons represent the first n components of the Fourier Series of a set of Gaussians, where each Gaussian’s center represents a different head direction on a cyclic axis (or in the paper a different location on a toroidal grid). The currently represented Gaussian can be shifted around by a rotation matrix applied by recurrent connections.

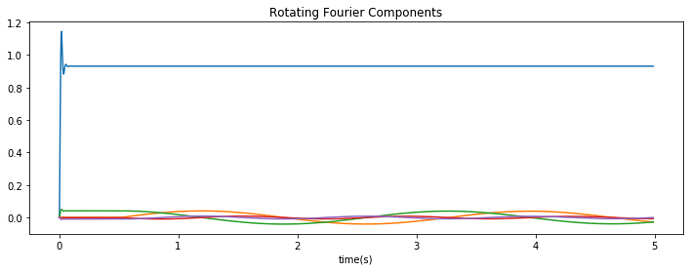
I managed to get everything to work using Direct neurons; the representation of the network, when a constant rotation speed is applied, looks like this:

The DC component in blue remains constant, while the other components oscillate as expected.

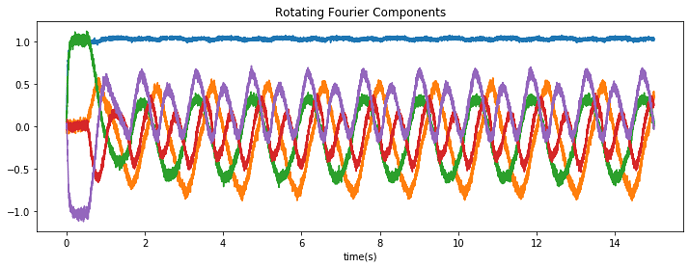
I am however struggling to get the network to work using LIF neurons, there are two problems I run into. The first is that when I set the encoders to the Fourier components of the Gaussians as in the paper (where each neuron represents a Gaussian with a different mean), the resulting activation when a Gaussian is provided as input is not a Gaussian anymore. My guess is that this is due to the scaling/normalization that is applied to the encoders, should I take this into account somehow?

Second, the authors of the paper managed to get a stable recurrent activity with a rather small time constant (0.005), which is not happening at all in my network; I only get some stable activity if increase the time constant to way higher. Is this just due to the bad representation of my neurons (I guess a longer time constant smooths out imperfections more)?

The code can be found here: https://github.com/Matthijspals/NengoSLAM/blob/master/HD_network.ipynb

Thank you so much for taking the time to look at this and please let me know if anything is unclear!

[MatthijsPals]

As my initial questions are probably a bit hard to answer without diving into the code, here are three more simple questions that should allow me to solve the problem at hand:

1. Can one in general use the same points for encoders and evaluation points?

2. Is it possible to get stable persistent activity using a recurrent connection with a small time constant?

3. The represented values of the (non-DC) Fourier coefficients are rather small, is this fine if the evaluation points are set accordingly? Or should I scale the to-be-represented values up/down? (I can imagine noise being disproportionally large for small represented values)

[tcstewar]

Hello Matthijs,

Very interesting question! I’ve tried playing with a few things, and I do believe this should be able to work, but I’m not quite sure what we need to adjust. I haven’t tried this before for a head-direction circuit – whenever I’ve needed something like that in the past I’ve used the controlled oscillator Controlled oscillator — Nengo 4.0.1.dev0 docs but the approach you’re trying here should also work and I’m not sure why it isn’t.

As for your more simple questions, let me try those:

1. Can one in general use the same points for encoders and evaluation points?

Yes, but be caureful. Encoders are automatically normalized to unit length. That way the encoder just specifies the preferred direction in state space, and doesn’t also affect the overall activity rate of the neurons. So in Nengo, the default encoders are on the surface of the N-dimensional hypersphere with the evaluation points are uniform inside the hypersphere. I think in the case you’re describing here, though, you only want to be able to represent points on that surface, so I think it’s okay.

One thing to watch out with evaluation points, though, is that they will be default be scaled by the radius. If you don’t want that behaviour you need to set scale_evaluation_points=False.

2. Is it possible to get stable persistent activity using a recurrent connection with a small time constant?

Yes, it just requires more neurons (roughly proportional the the reduction in time constant).

3. The represented values of the (non-DC) Fourier coefficients are rather small, is this fine if the evaluation points are set accordingly? Or should I scale the to-be-represented values up/down? (I can imagine noise being disproportionally large for small represented values)

That is a very good question, and I think it’s at the heart of what the problem is here. The decoder optimization is trying to reduce the RMSE of the representation, so I think the noise will be disproportionately large. I think it would help a lot to rescale those dimensions such that they are all in similar ranges.

[MatthijsPals]

Hi, thanks a lot for your reply!

@tcstewar

That is a very good question, and I think it’s at the heart of what the problem is here. The decoder optimization is trying to reduce the RMSE of the representation, so I think the noise will be disproportionately large. I think it would help a lot to rescale those dimensions such that they are all in similar ranges.

Scaling those dimensions seemed to fix most of the problem! :D. This is with spiking neurons:

@tcstewar

Yes, but be caureful. Encoders are automatically normalized to unit length. That way the encoder just specifies the preferred direction in state space, and doesn’t also affect the overall activity rate of the neurons. So in Nengo, the default encoders are on the surface of the N-dimensional hypersphere with the evaluation points are uniform inside the hypersphere. I think in the case you’re describing here, though, you only want to be able to represent points on that surface, so I think it’s okay.

One thing to watch out with evaluation points, though, is that they will be default be scaled by the radius. If you don’t want that behaviour you need to set scale_evaluation_points=False.

Can I then in this case just leave the radius as default as I anyway set the evaluation points and encoders manually?

Maybe I still have a slight misunderstanding here, but when I probe an ensemble the evaluation points set are also used to train the decoders used by the probe right? Yet neither a probe nor a ensemble has the scale_eval_points option - resulting in a scaled vector when I plot the probed ensemble after setting the radius.

[tcstewar]

Scaling those dimensions seemed to fix most of the problem!

Awesome!

Can I then in this case just leave the radius as default as I anyway set the evaluation points and encoders manually?

Yes! I often do that. The radius is really just a convenience function for doing that scaling, and if it’s not convenient I don’t use it…

Maybe I still have a slight misunderstanding here, but when I probe an ensemble the evaluation points set are also used to train the decoders used by the probe right? Yet neither a probe nor a ensemble has the scale_eval_points option - resulting in a scaled vector when I plot the probed ensemble after setting the radius.

That should only be an issue if you are setting eval_points on the Ensemble itself to something that you don’t want to have scaled. Although I’m not quite sure I’m picturing the situation right here…

[MatthijsPals]

@tcstewar

That should only be an issue if you are setting eval_points on the Ensemble itself to something that you don’t want to have scaled.

Yeah that was indeed the situation I was picturing, but I it is not a common situation and can be bypassed by scaling the eval_points for the ensemble with the inverse of the radius I guess.

Anyway thanks again, everything seems to run smoothly now!

[MatthijsPals]

Heey I am sorry to get back to this, but I cannot get this to work in two dimensions and I am not sure how to continue with finding the cause.

So in the 2d case, I want the network to represent the Fourier components of gaussians on a toroidal plane, for example:

I have set the encoders to represent the normalized Fourier components of the possible gaussians as a grid on the plane. The evaluation points were similarly set to the normalized Fourier components, now randomly sampled from the possible gaussians on the plane.

The problem is that after starting the simulation and initializing the network with a gaussian, the decoded representation (transformed back using the inverse Fourier transform) immediately drifts off to something like this:

Where could this drift come from?

I have tried to implement the network exactly as in: http://compneuro.uwaterloo.ca/files/publications/conklin.2005.pdf, who noted some attractor dynamics going on which made sure the representation would be gaussian.

The code for the network can be found here: https://github.com/Matthijspals/NengoSLAM/blob/master/Pos_network.ipynb

[tcstewar]

Hello again!

Hmm, interesting… It looks like everything should work — ah ha! I think I found the problem. Here’s how I debugged it a bit.

First, I tried running it with neuron_type=nengo.Direct() to see whether the underlying algorithm was correct. Here’s what I got with that:

So that looks great, meaning that function you’ve asked the neurons to approximate is correct, and the problem must be with how the neurons are approximating the desired function.

So, let’s look at the information the neurons are approximating when run with neuron_type=nengo.Direct():

plt.plot(sim.trange(), sim.data[hdp])

That looks great, but what jumps out at me is that there’s no way that data has a maximum radius of 1. Let’s plot the norm of the data:

plt.plot(sim.trange(), np.linalg.norm(sim.data[hdp], axis=1))

Okay, so we’re going to need a radius of around 4 if we want to represent things in this way. Let’s make that change and switch back to LIF neurons:

hd = nengo.Ensemble(neurons, dimensions=dim, eval_points=evalp, radius=4, encoders=encoders)
recur = nengo.Connection(hd, hd, eval_points = evalp, function = rotate, synapse=tau, scale_eval_points=False)

That seems to be closer to what we’re looking for! We could probably adjust that radius a bit (it might not have to be 4), but I think the overall system is working this way.

[MatthijsPals]

Thank you, this was indeed the problem! Also thanks for showing how you debugged it

[Jack]

Hello, I’ve read that article recently too, but I noticed that the link you shared is invalid now. Could you resend me the link to your code? Thanks.