Direct connections (with BCM rule) between individual neurons

Getting Started
1

Hi,
I would like to create some direct connections between individual neurons of two separate ensembles, but with the BCM rule. “Individual” means here: from one neuron to few others (but with noncontinuous indexes) - I treat an ensemble as a 2-dimensional array, as a picture shows:
Simple connections

There are some ways to do this:

ens1 = nengo.Ensemble(n_neurons=800, dimensions=1)
ens2 = nengo.Ensemble(n_neurons=400, dimensions=1)

Solution 1: I could create a huge transform matrix, defining connections by some value or by 0 which pretends there is no connection/no synapse between the two.

all_connections = nengo.Connection(ens1.neurons, ens2.neurons, transform=huge_all_to_all_matrix, learning_rule_type=...

But I assume that the zero-weight connections can be changed by BCM (due to postsynaptic activity and zero weight presynaptic spikes) - am I right? If so, it’s not a solution for me.

Solution 2: Create as many Connection instances (always one to one) as I need.

for i in ens1.neurons:
    for j in ens2.neurons:
        if should_create(i, j):
            nengo.Connection(ens1.neurons[i], ens2.neurons[j], transform=some_random_value(), learning_rule_type=...)

But I’m not sure is it good for performance? It also could be heavy for GUI (render thousands of connections).

Solution 3: Something in between - slicing - connect a particular neuron to a few rows separately.

for ...
    nengo.Connection(ens1.neurons[i], ens2.neurons[a:b], transform=random_vector_for_connecting_few_neurons, learning_rule_type=...)

But I think there is a better way. This solution isn’t clear and elegant, and still, there are many “Connection” instances.

Is there any better solution? I would like to also run the model on the OCL backend on NVidia GPU, and I’ve read a post that there is still some issue with Nengo sliced connections?

Btw. The network has 2-dimensional layers (ensembles as layers just for grouping purposes) - is there a better way to implement 2d layers (obviously not in an ensemble dimensionality manner)?

2

Hi @FilipD

I may have a solution for you, but first, I’ll get to your questions:

That is correct. With the BCM rule, even zero-weight connections can be changed by the weight update rule.

I’m not too sure about what the performance impact would be here, but I think there will be some performance decrease since (for regular Nengo) the numpy matrix operations are not being taken advantage of with multiple connections.

While this would have slightly better performance than solution 2, it should still perform worse that solution 1 since multiple connection updates is slower than 1 numpy matrix update for one connection.

Proposed Solution
So, having thought about it for a while, I believe that I may have a solution that fits your needs. My idea is to create what is essentially a copy of the BCM rule, with one critical change. The code that does the weights update for the BCM rule is this:

def step_simbcmmasked():
    delta[...] = np.outer(
        alpha * post_filtered * (post_filtered - theta), pre_filtered
    )

The computed delta matrix determines how the connection weight is changed (i.e., new_weight = old_weight + delta. So, for any connection that we don’t want updated, all we need to do is to zero out that corresponding value in the delta matrix. For everything else that we want updated, we just leave the value in the delta matrix there.
So, my idea is to create a separate mask matrix, and use the numpy multiply function to apply the mask to the delta matrix. If we have a 1 in the mask, the delta value is untouched, but, crucially, if we put a 0 in the mask, the corresponding value in the delta matrix is zeroed out, and thus the weight update for that connection will not happen. In essence, this code should do it:

def step_simbcmmasked():
    delta[...] = np.multiply(
        np.outer(alpha * post_filtered * (post_filtered - theta), pre_filtered),
        mask,
    )

Here is some code demonstrating the modified (masked) BCM rule, along with some test code:

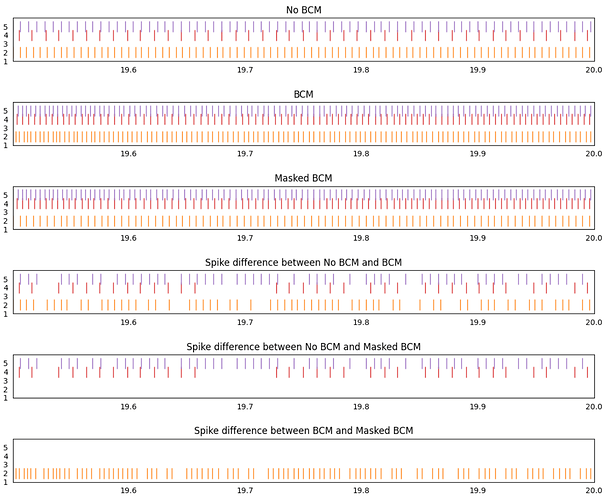
Here’s a plot demonstrating the code working:

image
image1386×1141 152 KB

The first 3 plots show the spiking output of a network with no learning rule, a network with the BCM learning rule, and a network with the masked BCM learning rule (where all inputs to neuron 2 have been masked).
The next 3 plots show any spiking activity difference between the different spike rasters. Any spike that appears at the same place in both spike raster will be removed from the final plot, but any spike that shows up in only one of the spike raster will show up in the final plot.
Comparing the no-bcm and bcm networks, we see that spike differences appear for all 3 active neurons in the post population. This is to be expected.
Comparing the no-bcm and masked bcm networks, we see that only neuron 4 and 5 show spike differences. Once again, this is to be expected since the weight updates for all connections into neuron 2 have been disabled, thus, the spike output of neuron 2 should be the same as in the no-bcm case.
Comparing the bcm and masked bcm networks, we see that since the bcm rule is applied to all neurons apart from neuron 2, only neuron 2 show a difference between these two cases. Since all 3 networks have the same seed, the BCM rule affects neuron 4 and 5 identically in both the bcm and masked bcm networks.

Additional Questions

The code I posted above currently only works in the Python Nengo. For NengoOCL, a custom ocl kernel is needed to implement the modified weight update. I’m not very familiar with OCL programming, so this may take some time for me to get working, although a quick look seem to indicate that it shouldn’t be too difficult. The existing BCM OCL kernel can be found here if you want to take a stab at it yourself. When I get the chance to test the OCL version I’ll update this thread.

Hmmm. Not really. Unlike something like tensorflow, Nengo doesn’t have a concept of “physical” arrangements of neurons within an ensemble. That being said, the advantage of that is that one ensemble can be physically interpreted as being any physical dimensionality (even a 3D arrangement if you want). But, the downside is that the physical arrangement of the neurons is up to the user to determine, by using the appropriate transformation matrices between connections. I’ll consult the other Nengo devs to see if they have any other ideas. :smiley:

3

One of the Nengo devs pointed out that while Nengo doesn’t natively support this kind of remapping, Numpy has various functions that can do this sort of mapping for you. As an example, Numpy’s ravel_multi_index function converts a tuple of indices, and a given dimensionality of the matrix into the equivalent single-dimensional (flat) index values.

1 Like
5

Alrighty! Here’s the NengoOCL-compatible implementation of the masked-BCM rule. NengoOCL has a slightly different implementation than Nengo. In Nengo, custom learning rules can be “registered” with the Nengo builder (that builds the Nengo simulator object), but for NengoOCL, you need to create a subclass of the NengoOCL simulator with calls to your custom learning rule inside it.

Here are the files you will need to run the masked-BCM rule in NengoOCL:

  • This file contains the custom openCL kernel, and the custom NengoOCL simulator that you will need to use: bcm_mask_ocl.py (5.4 KB)
  • This file contains some example test code (basically identical to the previous test code, but modified to run in NengoOCL): test_bcm_mask_ocl.py (6.1 KB)
    You will also require the original bcm_mask.py file since the Nengo model needs to be defined with the masked-BCM learning rule to work.
1 Like
6

Hi @xchoo

Wow! Thank you very much for all the knowledge you’ve posted and for the research you’ve made! Each of your posts is a part of the whole solution! :grinning:
Code examples are very helpful also, because, without the knowledge about the structure of the Nengo, it’s much harder to write new functions or classes.

Your proposed solution is great and definitely I’m gonna try it!

I still wonder about performance a little bit - is it possible to make it better - if somehow I could define continous ranges of indices between neurons (let’s say 1 neuron to 40 subsequent neurons) and have as much connections as neurons in upper layer (say 400), then I will have less to calculate (400 vectors of 40 elements = 16 000 synapses). But If make a big connection matrix (say 400 x 400 = 160 000 synapses), I’ll have a lot of zero-weigth synapses to calculate - only 1/10th of calculated will be useful. Am I right?

Yeah, I see. The Nengo focuses on the NEF approach, where we don’t have any 3D structure, rather functional structure, achieved by the whole ensembles. It’s good to hear, that my plans for using Nengo are ok.

Great, thanks for the developer and you! Instead of Numpy, I wanted to write my own functions to calculate indices, but the Numpy solution is better, at least for the performance. :grinning:

Ok, I’m gonna dive into it. First I have to try with Python Nengo, then with OCL.

Again, thank you very much, for such a big help! :smiley:

7

In some instances, using sparse computation does speed up the simulation speed compared to the naive implementation. In my testing, for a regular (i.e., non-learning) connection, there is little advantage to using a sparse representation and computation of the weight matrix. The Nengo code seems to be well optimized to handle large connection weight matrices, and trying to make the computation sparse would involve digging into the internals of Nengo, which is not a straightforward process.

However, where it probably speeds computation is with learning rules. You’ll have to experiment with it yourself, but you could modify the custom learning rule to only update the specific indices you want. Although, I’m not 100% sure if you need to make this change within the learning rule’s step_sim* function, or if you have to add additional logic into the build_* function, or if you have to go deeper into the Nengo guts. Doing a quick look, I believe this line of code is the bottleneck, and it is pretty embedded in the Nengo build tree, so modifying it to be faster, while possible, is complex. But, that is where something like NengoOCL comes in handy. From my quick experimentation, the performance impact in NengoOCL, while still present, is much less so that with standard Nengo.

8

Ok, thank you. I think I’ll make optimization tests after getting my basic functionality done. It’s good to hear that performance impact isn’t such big while using OCL. :slightly_smiling_face:

9

According to my first question - defining connections - I think, I’ve got one more solution. Similar to slicing, but with a smaller amount of separate connections (more sparse computation).

What if I just define one connection instance per upper-layer neuron, using the list of indices (as in the example below)? Then we’ve got 400 vectors of 40 elements (as in my previous post analogy), which is only 16 000 synapses to calculate (including BCM calculation).

layer_size = 400
ens1 = nengo.Ensemble(n_neurons=layer_size, dimensions=1)
ens2 = nengo.Ensemble(n_neurons=layer_size, dimensions=1)
for i in layer_size:
    list_of_neurons = calculate_list_of_neurons(i)  # eg. list_of_neurons = [0, 1, 2, 10, 11, 12, ...]
    initial_weights = caluculate_weights(i)  # proper shape matrix
    nengo.Connection(ens1.neurons[i], ens2.neurons[list_of_neurons], transform=initial_weghts)

I think, I’ll test both solutions, because I’m not sure which one is better for performance (can depend on hardware - CPU vs OCL) :slight_smile:

EDIT: Ok - this method is terrible, slows down drastically. It’s faster to calculate huge 400x400 matrix, even with BCM applied, than 400 separate connections 40x1 without BCM (on both - OCL and CPU).

10

Indeed! This is especially evident in OCL, since matrix operations are accelerated using the GPU (the GPU can do large matrix operations super fast since it partitions each element of the matrix to one compute element in the GPU, and the GPU has a lot of compute elements). However, if you make individual connections, NengoOCL is not yet smart enough to aggregate the computation into one big matrix operation, which results in 400 iterations in a for-loop (not acceleratable), instead of 1 giant matrix operation (acceleratable). This is probably where the slow down is occurring when you compare these two approaches.

A similar, but less dramatic effect happens on the CPU as well, since Numpy (which Nengo uses for most of it’s matrix operations) has special C libraries designed to quickly compute matrix operations on the CPU. Once again, for-loops break this optimization, but since the CPU has less “compute elements” than GPUs, the difference between the simulations speeds will be less dramatic than on the GPU.

11

Thanks, that clarifies such kind of behavior :slight_smile:

Currently, I’ve got a network with few layers, made of separate ensembles (which results in many separate connections). I consider aggregating them all into one ensemble, to utilize the GPU the most. However, having many ensembles makes it easier to debug in the GUI.
Maybe it’s a good idea for a new feature - virtual ensembles (made only for GUI)? :thinking:

Or maybe there is a possibility to somehow map the groups of neurons as separate ensembles, only for GUI?

12

There are disadvantages to making one big ensemble as well. As you mentioned, one of the disadvantages is that it makes the model exceedingly hard to work with. Also, with one big ensemble, the time it takes to solve for the weights increases exponentially w.r.t. the number of neurons in the ensemble. So, there’s typically a balancing point between the two approaches.

Virtual ensembles might work, but the issue there is the logic behind how to group ensembles into bigger blocks. I believe NengoDL has an optimizer (a graph optimizer, using TF’s underlying implementation), and a similar approach could be taken to improve the performance of NengoOCL models. Although, that is, admittedly, of lower priority for the Nengo dev team at the moment. The performance of NengoOCL is much faster than Nengo at the moment, and improving it is resource intensive, and we may look into this in the future. :slight_smile:

13

I see, so it depends on the particular numbers and used hardware.

I see, it was only a suggestion :smiley:

14

Yup. Although, in my experience, NengoOCL runs pretty quick, so if you have it running in NengoOCL, it’s pretty good. Even for massive models (I was constructing models with 6-7 million neurons at one point), the NengoOCL run (which runs on the GPU – took about half an hour for a 30-ish second run) was shorter than the time it took to build the model (which uses CPU resources – took about 1 - 1.5 hours to build the model). :laughing:

15

Wow :open_mouth: It’s a pity that building cannot be done with GPU :slight_smile:

16

Yeah, we did look into doing the model build process on the GPU, and it turned out to be non-trivial. Unfortunately, we had reshuffled around priorities and then never got back to it. Maybe when we have more manpower in the future, we’ll reopen this investigation. :smiley:

17

It would be great, someday :smiley: