Hi Alex,
In Nengo 3.1, we introduced three new neuron types that let you turn any rate neuron model into a spiking one. These are nengo.RegularSpiking, nengo.StochasticSpiking and nengo.PoissonSpiking. So to get a spiking tanh neuron type, you can just do something like nengo.RegularSpiking(nengo.Tanh()).
For the linear neuron, we don’t have this implemented in Nengo, but it’s really easy to implement yourself. You just make a neuron type whose output is its input.
Here’s an example of running both. For each type, I make an ensemble with one neuron, and then give it an input of -1 to 1 changing over time. For the Tanh neuron, we have it set up to have tau_ref = 0.0025 by default, which means that the firing will saturate at 400 Hz. I use a gain of 3 just to compress things a bit horizontally (this is equivalent to having the input go from -3 to 3).
For the linear neuron, I need to use a gain of 400 to get the input to go from -400 to 400. Since the linear neuron I’ve made has an output firing rate equal to its input, this results in firing rates from -400 Hz to 400 Hz.
import matplotlib.pyplot as plt
import nengo
class Linear(nengo.neurons.NeuronType):
def step(self, dt, J, output):
"""Implement the tanh nonlinearity."""
output[...] = J
spiking_tanh = nengo.RegularSpiking(nengo.Tanh())
spiking_linear = nengo.RegularSpiking(Linear())
with nengo.Network() as net:
u = nengo.Node(lambda t: t - 1)
ens_th = nengo.Ensemble(
1, 1, neuron_type=spiking_tanh, encoders=[[1]], gain=[3], bias=[0],
)
nengo.Connection(u, ens_th)
probe_th = nengo.Probe(ens_th.neurons, synapse=nengo.Alpha(0.01))
ens_lin = nengo.Ensemble(
1, 1, neuron_type=spiking_linear, encoders=[[1]], gain=[400], bias=[0],
)
nengo.Connection(u, ens_lin)
probe_lin = nengo.Probe(ens_lin.neurons, synapse=nengo.Alpha(0.01))
with nengo.Simulator(net) as sim:
sim.run(2.0)
plt.plot(sim.trange(), sim.data[probe_th], label="spiking tanh")
plt.plot(sim.trange(), sim.data[probe_lin], label="spiking linear")
plt.legend()
plt.show()
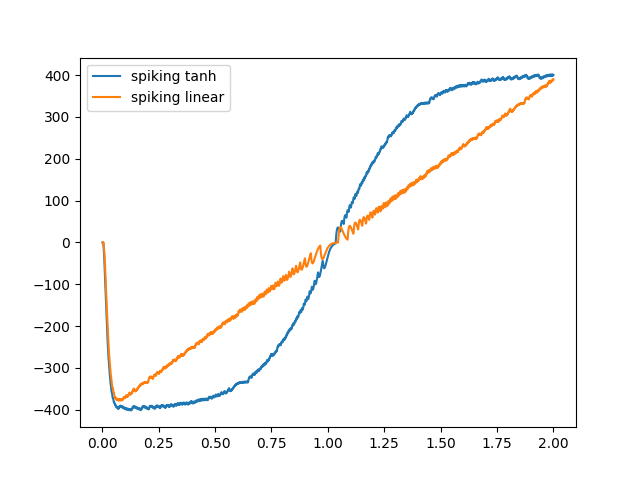
Note how things get a little “noisy” around where the curves cross y = 0. This is because I’m filtering the output spike train to get the curve that I display, and around y = 0 the neurons have low firing rates, so there’s only a few spikes in that region.
One other thing to keep in mind is that all of this allows negative spikes. That is, a single neuron essentially has two kinds of spikes it can fire, a positive one or a negative one. This is how a single neuron can represent both positive and negative signals. This is not biologically plausible; this behaviour is never seen in the brain. It also won’t work on a lot of neuromorphic hardware.
A more biologically plausible approach might consist of using multiple neurons of a standard neuron type (e.g. nengo.LIF) to represent one tanh or linear neuron. This uses the same “population coding” idea that the NEF uses to represent and transform values (see the NEF summary notebook for more details). The number of neurons you need depends on the shape of the function you want to represent, and how accurately you want to represent it. We’ve used three LIF neurons to represent a sigmoid neuron before; by optimizing the parameters of the LIF neurons, we were able to represent it quite accurately. I expect you’d be able to do something similar to represent a Tanh neuron with a handful of LIF neurons. For your linear neuron, I expect you’d actually need more LIF neurons than for the Tanh neuron, since the LIF tuning curve naturally resembles part of a Tanh curve more closely than it does a line. You could always use RectifiedLinear neurons to represent the line, though, in which case you’d just need two (one for the positive, and one for the negative). With all these approximations, you’re using more than one neuron per nonlinearity in your network, so these networks can get large quite quickly. This is why we developed the approach of training with LIF neurons, so that we could let the network learn how best to use this neuron type, rather than trying to do the approximation ourselves.
