Hi @RohanAj, and welcome to the Nengo forums!
I’ll attempt to address your questions below:
The difference between these two connection types has to do with the way the Neural Engineering Framework (NEF) formulates connections. In the first case, Nengo is constructing a connection where the connection weight matrix has effectively been factored into multiple parts: encoders, decoders, and a transformation matrix. You can read more about what these components do here and here.
Conversely, the connection with the .neuron attribute makes a connection from to/from an ensemble of neurons bypassing the encoders and/or decoders for that ensemble. Note that Nengo allows for the .neuron attribute to be used as the source or target (or both) of the connection, as discussed here.
If the two connection methods are created with mathematically identical connection matrices (with the .neurons connections, you’ll need to account for the encoders and decoders in the connection weight matrix), then there is no difference between the network outputs. Computationally, the networks will differ slightly as the neuron-to-neuron connection requires Nengo to use the entire connection weight matrix to compute the connections while encoded-decoded connections can use the factored encoder and decoder weights, which is more efficient.
The Nengo documentation includes several examples of how to include learning in your Nengo networks. To learn input-output pairs, this example in particular may interest you.
The code below illustrates how learning can be done with fully connected ensembles in Nengo.
with nengo.Network() as model:
sin = nengo.Node(lambda t: np.sin(t * 4))
pre = nengo.Ensemble(100, 1)
post = nengo.Ensemble(100, 1)
error = nengo.Ensemble(100, 1)
nengo.Connection(sin, pre)
nengo.Connection(sin, error, transform=-1)
nengo.Connection(post, error)
conn = nengo.Connection(pre, post, solver=nengo.solvers.LstsqL2(weights=True),
transform=0)
# The solver argument, where `weights=True` initializes this connection as a
# fully connected weight matrix connection.
# Transform is set to 0 to initialize all connection weights to 0
conn.learning_rule_type = nengo.PES()
nengo.Connection(error, conn.learning_rule)
To extract the weights from the example code above, you’ll first have to create a Nengo simulator object, and then run the simulator. The code below does this, then extracts the code after the simulation has completed:
# Create and run the Nengo simulation
with nengo.Simulator(model) as sim:
sim.run(10)
# Extract the weights after the simulation run
learned_weights = sim.model.params[conn].weights
You can input spikes to an ensemble of neurons using a nengo.Node. Keep in mind that when you do this, the spike value should be 1/dt, where dt is the dt used for your Nengo simulation (defaults to 0.001s) The following code is an example of how to do this (the spike_func is just a random spike generator that doesn’t really do anything but produce random spikes for the first 0.25s of the simulation)
def spike_func(t):
if np.random.random() < 0.5:
return 1 / dt and t < 0.25
else:
return 0
with nengo.Network() as model:
s_in = nengo.Node(spike_func)
ens = nengo.Ensemble(1, 1, intercepts=[0])
nengo.Connection(s_in, ens.neurons)
To record spikes from any ensemble in a Nengo model, use the nengo.Probe functionality, like so (this carries from the previous example code):
with model:
p_spikes = nengo.Probe(ens.neurons)
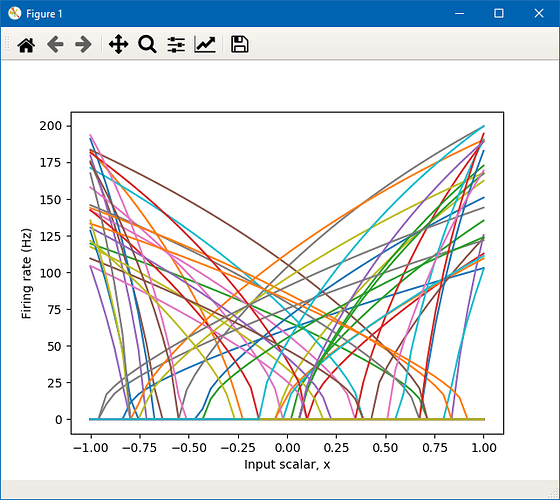
By default, Nengo generates randomized values for the biases and gains for each neuron in an ensemble. This in turn randomly generates maximum spike rates and intercepts for the neural response curves.
You can change the spike rate of neurons by specifying the max_rates parameter when creating the neural ensemble. The following code generates an ensemble of 50 neurons with firing rates from 100-200 Hz.
from nengo.dists import Uniform
with nengo.Network() as model:
ens = nengo.Ensemble(50, 1, max_rates=Uniform(100, 200))
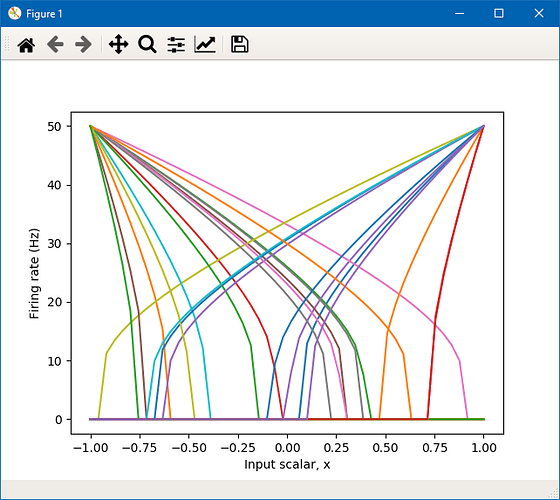
You can fix all of the neuron firing rates to the same value by using the Choice distribution. The code below shows how to create an ensemble of 25 neurons, all of them with maximum rates of 50 Hz.
from nengo.dists import Choice
with nengo.Network() as model:
ens = nengo.Ensemble(25, 1, max_rates=Choice([50]))