Challenge #1: Clean 0 and 1 output

Examples & Tutorials
1

Welcome to challenges!

The idea is to have a series of simple problems, presented every so often, where people can discuss different circuits and implementations / weigh the pros and cons of various approaches. The goal is to hopefully learn some new techniques for neural circuit design and generate a set of efficient, robust solutions to various problems.

Answers should be posted with code and simulation results!

The first challenge is to generate a circuit that transforms an input signal into a clean 0 if it’s below .5, and a clean 1 if it’s above .5.

The input to the system is nengo.Node(lambda x: np.cos(x)*.5+.5) and the system should run for 6 seconds.

Go!

1 Like
2

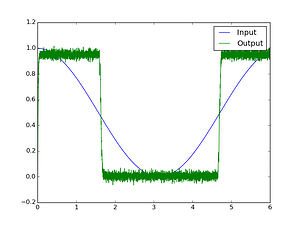
Here’s one possible solution:

import nengo
import numpy as np

model = nengo.Network()
with model:
    stim = nengo.Node(lambda x: np.cos(x)*.5+.5)
    
    b = nengo.Ensemble(n_neurons=50, dimensions=1, 
        intercepts=nengo.dists.Uniform(.5, 1),
        encoders=[[-1]]*50)
    out_b = nengo.Ensemble(n_neurons=50, dimensions=1)
    
    output = nengo.Ensemble(n_neurons=50, dimensions=1)
    
    nengo.Connection(stim, b, function=lambda x: x-1)
    
    nengo.Connection(b, out_b.neurons, 
        function=lambda x: 1,
        transform=[[-3]]*out_b.n_neurons)
    
    nengo.Connection(out_b, output, function=lambda x: 1)

    probe_input = nengo.Probe(stim)
    probe_output = nengo.Probe(output, synapse=.01)

sim = nengo.Simulator(model)
sim.run(6)

import matplotlib.pyplot as plt
plt.plot(sim.trange(), sim.data[probe_input])
plt.plot(sim.trange(), sim.data[probe_output])
plt.legend(['Input', 'Output'])
plt.show()

figure_1.png800×600 34.6 KB

3

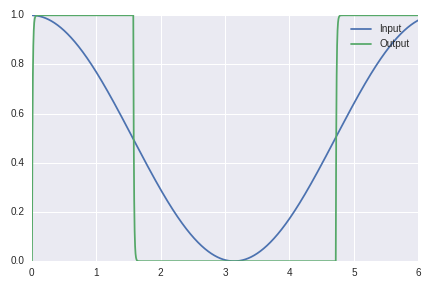
Here’s another one and look it’s perfect:

import nengo
import numpy as np

model = nengo.Network()
with model:
    stim = nengo.Node(lambda x: np.cos(x)*.5+.5)
    
    output = nengo.Node(lambda t, x: 0 if x < 0.5 else 1, size_in=1)
    nengo.Connection(stim, output)
    
    probe_input = nengo.Probe(stim)
    probe_output = nengo.Probe(output, synapse=.01)

sim = nengo.Simulator(model)
sim.run(6)

import matplotlib.pyplot as plt
plt.plot(sim.trange(), sim.data[probe_input])
plt.plot(sim.trange(), sim.data[probe_output])
plt.legend(['Input', 'Output'])
plt.show()

Ok, I’m just kidding with a node you can implement anything. :wink:

1 Like
4

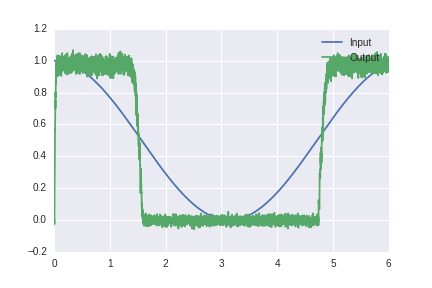
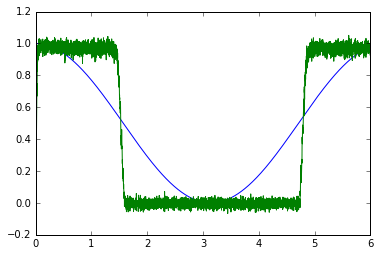
This is an actual solution with neurons:

import nengo
import numpy as np

model = nengo.Network()
with model:
    stim = nengo.Node(lambda x: np.cos(x)*.5+.5)
    
    threshold = nengo.Ensemble(
        75, 1,
        intercepts=nengo.dists.Exponential(0.3, 0.5, 1.),
        encoders=nengo.dists.Choice([[1]]),
        eval_points=nengo.dists.Uniform(.5, 1.))
    nengo.Connection(stim, threshold)
    
    output = nengo.Ensemble(75, 1)
    nengo.Connection(threshold, output, function=lambda x: 0 if x < 0.5 else 1)
    
    probe_input = nengo.Probe(stim)
    probe_output = nengo.Probe(output, synapse=.01)

sim = nengo.Simulator(model)
sim.run(6)

import matplotlib.pyplot as plt
plt.plot(sim.trange(), sim.data[probe_input])
plt.plot(sim.trange(), sim.data[probe_output])
plt.legend(['Input', 'Output'])
plt.show()

1 Like
5

Interesting! Compressed down to one population, using 25 less neurons!
Is the Exponential more effective here than a Uniform?

6

Actually I though I was using the same number of neurons …

Yes, see here and here.

7

It should be noted that with the nengo presets (in the dev version of nengo), you can implement the network like so:

import nengo
import numpy as np

model = nengo.Network()
with model:
    stim = nengo.Node(lambda x: np.cos(x)*.5 + .5)
    
    threshold_val = 0.5
    with nengo.presets.ThresholdingEnsembles(threshold_val):
        threshold = nengo.Ensemble(75, 1)
    nengo.Connection(stim, threshold)
    
    output = nengo.Ensemble(75, 1)
    nengo.Connection(threshold, output, function=lambda x: 0 if x < 0.5 else 1)
    
    probe_input = nengo.Probe(stim)
    probe_output = nengo.Probe(output, synapse=.01)

sim = nengo.Simulator(model)
sim.run(6)

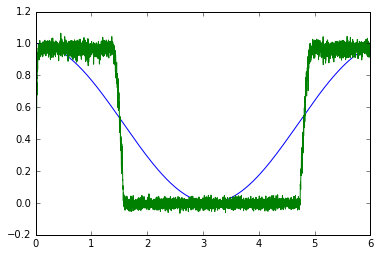
There is a slight difference in the first parameter of the Exponential distribution, but that just affects the steepness of the transition point.

Without preset:

With preset:

8

It should also be noted that the presets are not part of any official release yet.

9

I’ve updated my comment. :smile:

10

Great tutorial Jan! Super well put together, thanks for the link!