You generally have the right idea, and your network is very close to working! 
The three components you need: the integrator that produces the ramp, the threshold detector, and the reset signal generator are there, but there is one key feature of the reset signal generator that you need to implement.
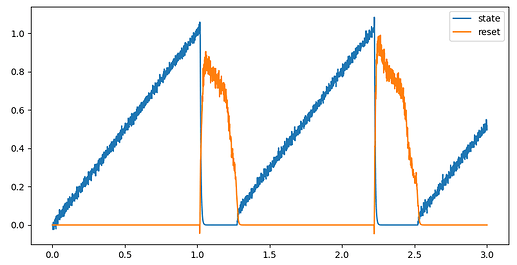
If you look at the output of your reset signal you see that it quickly goes up to about 1.2, but then it stays there. Compared to the plot I included in my first reply, you’ll notice that my ramp signal quickly goes up, but then after some time, starts to decay back to 0. Introducing this decay is very simple, but first, let us understand why the reset signal goes to ~1.2 and stays there.
In your code, this code implements the reset signal:
ramp_reset = make_thresh_ens_net(0.07, thresh_func=lambda x: x)
nengo.Connection(ramp_reset.output, ramp_reset.input)
If we look at the feedback connection, we see that it is using the default transform value, which is 1. Thus, any output of the ramp_reset network gets fed back into to the input of ramp_reset and it is able to maintain a value even after the thresh input goes to 0. This is why the output of ramp_reset quickly goes to ~1.2, but then stays there.
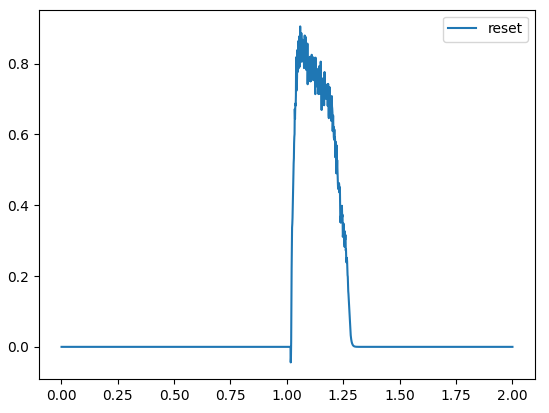
To make the ramp_reset signal decay back to 0 after some time, all we have to do is ensure that the feedback connection does not feed the full output signal back to the input. This is done by applying a transform value that is less than 1 on the feedback connection. For your network, I found that a value of 0.955 works, but you can experiment with it on your own to find a value suitable for you.
ramp_reset = make_thresh_ens_net(0.07, thresh_func=lambda x: x)
nengo.Connection(ramp_reset.output, ramp_reset.input, transform=0.955)
Once you do this, you will see that the ramp signal decays back down to 0 after some time:
And, when we look at this in the context of the whole network, we see that the ramp signal resets, but the cycle repeats!