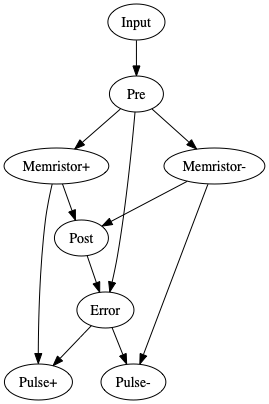
Thanks for the context! You’re right that with the way you have things set up, your connections from pre are using the encoded vectors. Am I correct in assuming that you would like to be using neural activities and raw connection weight matrices rather than decoded values and vectors? For everything except for the connections to/from error? If so, here is one way to set things up.
with model:
inp = nengo.Node(
output=lambda t: int(6 * t / 5) / 3.0 % 2 - 1, size_out=1, label="Input"
)
pre = nengo.Ensemble(1, dimensions=1, label="Pre")
post = nengo.Ensemble(1, dimensions=1, label="Post")
err = nengo.Ensemble(100, dimensions=1, label="Error")
memristor_plus = nengo.Node(
exc_synapse.filter,
size_in=pre.n_neurons,
size_out=post.n_neurons,
label="Memristor+",
)
memristor_minus = nengo.Node(
inh_synapse.filter,
size_in=pre.n_neurons,
size_out=post.n_neurons,
label="Memristor-",
)
pulse_plus = nengo.Node(
exc_synapse.pulse,
size_in=post.n_neurons + err.dimensions,
size_out=post.n_neurons,
label="Pulse+",
)
pulse_minus = nengo.Node(
inh_synapse.pulse,
size_in=post.n_neurons + err.dimensions,
size_out=post.n_neurons,
label="Pulse-",
)
nengo.Connection(inp, pre)
nengo.Connection(pre.neurons, memristor_plus, synapse=None)
nengo.Connection(pre.neurons, memristor_minus, synapse=None)
nengo.Connection(memristor_plus, post.neurons, synapse=None)
nengo.Connection(memristor_minus, post.neurons, synapse=None, transform=-1)
nengo.Connection(pre, err, function=lambda x: x, transform=-1)
nengo.Connection(post, err)
nengo.Connection(memristor_plus, pulse_plus[: post.n_neurons], synapse=None)
nengo.Connection(memristor_minus, pulse_minus[: post.n_neurons], synapse=None)
nengo.Connection(err, pulse_plus[post.n_neurons :])
nengo.Connection(err, pulse_minus[post.n_neurons :])
The main things that I’ve changed are:
-
The connections to/from pre and post use pre.neuron and post.neurons, which gives you the underlying neural activities rather than the decoded values. This allows you to modify the number of neurons in the pre and post ensembles while still being able to use the decoded pre and post vectors to compute error.
-
Since you can vary the number of neurons in pre and post now, I used pre.n_neurons and post.n_neurons for size_in and size_out.
-
The connections to pluse_plus and pulse_minus now send the filtered neural activites from memristor_plus and memristor_minus as the first dimension(s) and the error signal from err as the last dimension. This allows you to separate out these two inputs. If you provide both to the same dimension, they will be summed together. By separating it out into separate dimensions, you can deal with them internally in Memristor like so:
def pulse(self, t, x):
filtered_activities = x[: post.n_neurons]
err = x[post.n_neurons :]
...
I verified that the above model works with a mocked out Memristor class:
class Memristor:
def filter(self, t, x):
return x
def pulse(self, t, x):
return x[: post.n_neurons]
exc_synapse = Memristor()
inh_synapse = Memristor()
One thing to note when you run this model is that your input function is not going to change for a relatively long time. The default timestep in Nengo is 0.001 (which represents 1 millisecond) so your input won’t change for the first ~ 0.83 simulated seconds, or around 830 timesteps. You can always raise the dt when you create the simulator with nengo.Simulator(model, dt=0.5) if you’re expecting a different timestep size.
Also, apologies for changing the code formatting, my editor auto-formats Python code and I forgot to turn that off!