Dear all,
I need to branch a nengo connection for an nengo.ensemble
nengo.connection(ens1, ens2)
or
nengo.connection(ens1, ens3)
as result of a SPA - BG-THAL decision: ifmax …
that means:
spa.ifmax (…1…)
nengo.connection(ens1, ens2)
spa.ifmax (…2…)
nengo.connection(ens1, ens3)
but I can not define nengo.connections for ensembles in a spa-context. (only for spa.buffers)
How can I solve that problem?
Best
Bernd
Hi @bernd,
Unfortunately, if you want to use the NengoSPA library to build a BG-Thalamus control circuit, the spa.ActionSelection() rules only work with spa.State objects (note here, I’m using the NengoSPA library syntax here, and not the nengo.spa library, which has been deprecated).
However, under the hood, spa.State objects are essentially Nengo ensembles, and can be interacted with them as such. The only difference to the interaction is that they contain a .input and a .output object to connect from/to them, rather than connecting to the object themselves.
So, you could have something like this:
with spa.Network() as model:
....
ens1 = spa.State(dimensions)
ens2 = spa.State(dimensions)
ens3 = spa.State(dimensions)
# These are your action selection rules
with spa.ActionSelection() as action_sel:
spa.ifmax("1", spa.dot(...), ens1 >> ens2)
spa.ifmax("2", spa.dot(...), ens1 >> ens3)
# Vanilla Nengo ensemble
vens1 = nengo.Ensemble(n_neurons, dimensions)
# Example connection between spa.State and ensemble
nengo.Connection(ens2.output, vens1)
If you don’t want all of the bells and whistles that come with the spa.State object, you can also create your own custom spa module that contains just one Nengo ensemble, although I suspect that you shouldn’t need to do this. If there is a reason why you’d need to connect Nengo ensembles (rather than SPA modules) in your BG decision loop, let me know, and I’ll see if there’s a proper workaround for it.
Dear Xuan
thank you for your quick response.
Yes that would be a great solution, if the number of neurons within the ensemble are comparable with that of the state buffer per dimension.
But the number of neurons per dimension in the state buffer is n=50 auf I have D=256 dimensions. That defines my SPA. My SPA models all cortical levels including the mental lexicon in my word-production scenarios (semantic and phonological level). But on the motor level (for modeling speech articulation) I need a connection between syllable oscillators, defined as
BA_oscillator = nengo.Ensemble(m, dimensions=2, intercepts=Uniform(0.3,1), encoders=encoders)
with m=2500
(example here is for the syllable /ba/)
and gesture oscillators (for producing moments like labial closure etc.), defined as
sa_lab_constr = nengo.Ensemble(N, 1)
with N= 2000
(example here is for a labial closing gesture , which realizes the sound /b/)
The syllable oscillator starts the gesture (the speech sound within the syllable) for example like:
nengo.Connection(BA_oscillator, sa_lab_constr, function=BA_signal_sa_lab_constr, transform=[cons_vel])
But this connection is fix and I need to make it flexible:
Oscillators need to be defined in the next version of my model not for each combination of consonants and vowels like ba, da, ga, bi, di, go and so on, but just for type of syllable (like here: CV) C=consonant and V=vowel (in contrast to something like CVC for realizing /bat/, /dat/ etc.)
So: I want to define only few syllable oscillators for different TYPES of syllables and the neural connections between syllable oscillator and gesture (these connections define the timing, i.e. the staring time for each sound gesture) needs to be controlled by a kind of gaiting, which is controlled from SPA-level by the type of sound sequence (e.g. /ba/ or /da/ or /bi/ or /di/ etc.)
So: I have a neural connection from syllable oscillator to different consonants (/b/, /d/, or /g/; that means: labial, apical and dorsal)), like:
nengo.Connection(CV_oscillator, sa_lab_constr, function=BA_signal_sa_lab_constr, transform=[cons_vel])
nengo.Connection(CV_oscillator, sa_api_constr, function=BA_signal_sa_lab_constr, transform=[cons_vel])
nengo.Connection(CV_oscillator, sa_dors_constr, function=BA_signal_sa_lab_constr, transform=[cons_vel])
but I want that only that connection becomes active, And this connection represents the concrete syllable under production: /ba/, /da/ or /ga/.
And that information (syllable = /ba/, /da/ or /ga/) is represented by a SPA-S-pointer and thus, my idea was: I have to select the correct nengo_connection between syllable oscillator and gestures within the syllable on the BG-THAL spa.ActionSelection() level.
Do you have an idea for a solution for this special case: (connection for ensembles with high n_neurons controlled by action selection of the SPA component with n_neurons per dimension not higher than 50) ?
Perhaps there is a chance to control the connection between oscillator and ensembles in a different way, if you have all detailed infos concerning that nengo.connection.
I try to give that here as well in addition:
BA_func_sa_lab_constr = piecewise({0:[0], 0.3:[0.8], 0.48:[0]}) # C1 initial: /b/
BA_func_sa_final = piecewise({0:[0], 0.6:[1.0], 0.68:[0]}) # final
BA_func_sa_vow_A = piecewise({0:[0], 0.3:[0.7], 0.7:[0]}) # vowel A
def BA_signal_sa_lab_constr(x):
theta = math.atan2(x[1], x[0])
t = theta/ (2*np.pi) + 0.5
return BA_func_sa_lab_constr(t)
def BA_signal_sa_final(x):
theta = math.atan2(x[1], x[0])
t = theta/ (2*np.pi) + 0.5
return BA_func_sa_final(t)
def BA_signal_sa_vow_A(x):
theta = math.atan2(x[1], x[0])
t = theta/ (2*np.pi) + 0.5
return BA_func_sa_vow_A(t)
BA_oscillator = nengo.Ensemble(m, dimensions=2, intercepts=Uniform(0.3,1), encoders=encoders)
# Set recurrent connections on oscillators with parameters for adjusting oscillation frequency.
tau = 0.025 # Adjust to avoid multiple oscillations.
# needs to be adjusted together with freq, if freq. is above 2.0 Hz!
freq = 1 # 2.0
omega = tau*2*np.pi*freq
nengo.Connection(BA_oscillator, BA_oscillator, transform=[[1, -omega], [omega, 1]], function=zone, synapse=tau)
N = 2000 # 2000
# Premotor trajectory generators for speech actions "sa"
sa_lab_constr = nengo.Ensemble(N, 1) # b, p, m,
sa_api_constr = nengo.Ensemble(N, 1) # d, t, n,
sa_dor_constr = nengo.Ensemble(N, 1) # g, k, N,
# Connect oscillators to speech actions
nengo.Connection(BA_oscillator, sa_lab_constr, function=BA_signal_sa_lab_constr, transform=[cons_vel])
nengo.Connection(BA_oscillator, sa_final, function=BA_signal_sa_final, transform=[final_vel])
nengo.Connection(BA_oscillator, sa_vow_A, function=BA_signal_sa_vow_A, transform=[vow_vel])
# Recurrently connect trajectory generators to allow adjustable filtering
nengo.Connection(sa_lab_constr, sa_lab_constr, transform=[1-cons_vel])
nengo.Connection(sa_api_constr, sa_api_constr, transform=[1-cons_vel])
nengo.Connection(sa_dor_constr, sa_dor_constr, transform=[1-cons_vel])
and in addition the connection, which activates a syllable:
nengo.Connection(model.motor_syll_init.selection.output[14], BA_oscillator, transform=[[-1],[0]])
this is driven by the activation of the SPA-S-pointer:
motor_syll_init, and its output 14 is the syllable-/ba/-S-poiner.
Best
Bernd
Hi @bernd,
After reading the description of what you are trying to achieve, I believe there are two methods for doing things. The first method would be the easiest to implement, and that is to simply convert your oscillators into SPA modules. The second method would be more complex to implement but may be easier to expand, and that is to use a system similar to the one in Spaun (I describe this system in my thesis in Section 3.3.8) where the BG rules update some “state” representation. This “state” representation can then be used to generate control signals that are then used to directly inhibit connections between the oscillators (or inhibit the oscillators themselves). I’ll describe these two methods in more detail below.
The Module Approach
In this approach, you basically turn the various oscillator types (you have one for the syllable, and one for the gestures, it looks like?) into SPA modules. Doing so is quite simple, all you need to do is create a subclass of the nengo_spa.Network class, and set the vocabulary, inputs and outputs correctly. Here’s an example for a regular Nengo ensemble:
class EnsembleModule(Network):
vocab = VocabularyOrDimParam("vocab", default=None, readonly=True)
def __init__(self, ens_params={}, vocab=Default, **kwargs):
super(EnsembleModule, self).__init__(**kwargs)
with self:
self.ens = nengo.Ensemble(**ens_params)
self.input = self.ens
self.output = self.ens
self.declare_input(self.input, None)
self.declare_output(self.output, None)
You’ll notice in the code above that the default vocabulary for the EnsembleModule is None, so it can’t use any of the fancy vocabulary stuff in the BG rules (but that’s likely not needed). If you want to connect to or from the EnsembleModule, simply connect to the .input or .output attributes, e.g.,:
# Input signal for ensembles
inp2 = nengo.Node(WhiteSignal(60, 10), size_out=1)
source = EnsembleModule(ens_params={"n_neurons": 50, "dimensions": 1})
nengo.Connection(inp2, source.input)
And as SPA modules, they can be used in the BG rules without much change:
# Ensembles (ensemble modules)
dest1 = EnsembleModule(ens_params={"n_neurons": 50, "dimensions": 1})
dest2 = EnsembleModule(ens_params={"n_neurons": 50, "dimensions": 1})
dest3 = EnsembleModule(ens_params={"n_neurons": 50, "dimensions": 1})
# Example BG rule set. Given the semantic pointer represented by the `inp` module,
# the BG will route information from `source` to the desired `dest` module.
# The "Default" rule is added so that when `inp` has no value, `source` is routed
# to nothing.
with spa.ActionSelection() as action_sel:
spa.ifmax("Default", 0.5)
spa.ifmax("EN1", spa.dot(inp, spa.sym.ENABLE1), source >> dest1)
spa.ifmax("EN2", spa.dot(inp, spa.sym.ENABLE2), source >> dest2)
spa.ifmax("EN3", spa.dot(inp, spa.sym.ENABLE3), source >> dest3)
So, the idea with this approach is to take the template SPA module I wrote above and replace the nengo.Ensemble with code to create your specific oscillators. Then, using it with the rest of the SPA model should be pretty straight forward.
Here’s some code where I use the EnsembleModule to create a basic switch.
module.py (3.7 KB)
The switch is controlled by the semantic pointer representation in the inp state. When inp == ENABLE1, the BG routes source to dest1, and when inp == ENABLE2, the BG routes source to dest2, and similarly for source to dest3 when inp == ENABLE3.
This graph shows the results:
As you can see from the plots above, the simple model works quite well. There are, however, some properties of the network that can be observed. First, due to the way the routing connections are made, a delay of about 15ms is introduced between the source and dest ensembles. Second, there is an additional delay of about 50ms from when the semantic pointer in inp changes to when the routing itself switches (this is the “standard” 50ms “decision” time of the BG network).
Control Hierarchy Approach
With the control hierarchy approach, the idea is to use the BG rules to update the semantic pointer in some State module, rather than controlling the routing directly. You can use the state of the State module to generate control signals that do things like inhibit specific components in your system (e.g., inhibit the oscillators). If you set up a chain like so:
oscillator → ensemble → oscillator
and feed the inhibitory control signal to the middle ensemble, you can turn the ensemble on / off to function as a gate (controlling the flow of signals from one oscillator to another). To expand, if you have something like this (one source oscillator connected to multiple ensembles, each connected to a downstream oscillator):
.-> ensemble --> oscillator
oscillator -+-> ensemble --> oscillator
`-> ensemble --> oscillator
You can use the control signals to inhibit select ensembles to control where the signal from the source oscillator ends up.
Here’s some code of the previous example re-written as a control hierarchy:
control.py (7.3 KB)
And here is what the output looks like:
From the graphs, you will see that the ~50ms “decision” time for the BG circuit is still present (this is pretty much unavoidable). But, because the control hierarchy is directly inhibiting the destination ensembles, there is very little delay between the source and destination signals.
Also, if you look at the “ENABLE3” stage, I modified the ruleset to allow source–>dest1 and source–>dest3 (at the same time!). Such complex routing is more difficult (if not impossble) to set up with the previous approach because the BG rule set only allow 1 routing per rule (i must double check this).
With the control hierarchy, doing multiple routing is as easy as putting both the ENABLE1 and ENABLE3 semantic pointers into the control state module. Since the control signals are generated based on the semantic pointers in the control state module (just using dot products), you just put the semantic pointer states you want into the control state module, and the control signals will auto-generate from them. This makes the system more flexible and easy to extend!
Let me know if you have any questions! 
Hi Xuan
thank you for your detailed answer.
I am starting to adapt solution 1 (Spa module) to my source code now 
I will be back with some questions later.
Best
Bernd
always the same …
if I have posted a problem, I directly get an idea for the solution by myself
Sorry for deleting thus many posts … but may be, I need. to formulate the problem in detail in order to be able to solve it
Best
Bernd
Dear Xuan
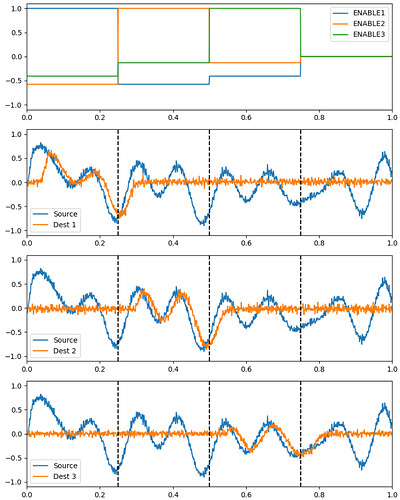
I was able to implement your advised solution 1 (convert ensembles in SPA module. ensembles) and have attached two figures which show a syllable oscillator and the coupled speech actions (just look at row “oscillators” and “speech actions”).
In case of the syllable oscillator for /pi/ (two lines per oscillator → so: only one oscillator is active!) , three actions are activated (via BG-Thal): the vowel action for /i/ → sa_vow_i (magenta), the consonant action for /p/ → sa_constr_lab (labial cnstriction: dark blue) and a action which signals the end of the syllable → sa_final (light blue).
The rest is just concerning the connection of the syllable oscillator with the speech action oscillator for the vowel I (magenta line in row" speech actions")
Now I address the problem of activating the speech actions (here the vowel action):
To my knowledge a direct formulation of the direct neural connection is not possible in the BG-Thal (in the action selection part). The connection is:
nengo.Connection(BI_oscillator.output, sa_vow_I.input, function=CV_signal_sa_vow_I, transform=[vow_vel])
with:
def CV_signal_sa_vow_I(x):
theta = math.atan2(x[1], x[0])
t = theta/ (2*np.pi) + 0.5
return CV_func_sa_vow_I(t)
and:
CV_func_sa_vow_I = piecewise({0:[0], 0.3:[0.7], 0.7:[0]})
Because this connection is thus complex, to my knowledge it can not be written as
BI_oscillator.output >> sa_vow_I.input
and thus can not be used directly in the action selection part of the source code.
Thus, I define two further SPA module ensembles called:
connIn_syll2sa_vow_I = EnsembleModule(ens_params={"n_neurons": n_ens_syll2sa, "dimensions": 2})
connOut_syll2sa_vow_I = EnsembleModule(ens_params={"n_neurons": n_ens_syll2sa, "dimensions": 2})
and I define the connection between syllable oscillator for bi and speech action vor vowel i as:
nengo.Connection(BI_oscillator.output, connIn_syll2sa_vow_I.input)
connIn_syll2sa_vow_I >> connOut_syll2sa_vow_I
nengo.Connection(connIn_syll2sa_vow_I.output, sa_vow_I.input, function=CV_signal_sa_vow_I, transform=[vow_vel])
and now the line
connIn_syll2sa_vow_I >> connOut_syll2sa_vow_I
can be part of the BG-Thal action selection part in the source code.
But doing so (even If I use the source code as written above without running the neural connection
connIn_syll2sa_vow_I >> connOut_syll2sa_vow_I
within the BG-Tal action selection part of the module (but let it run permanently like written above),
I get an artifact, which is:
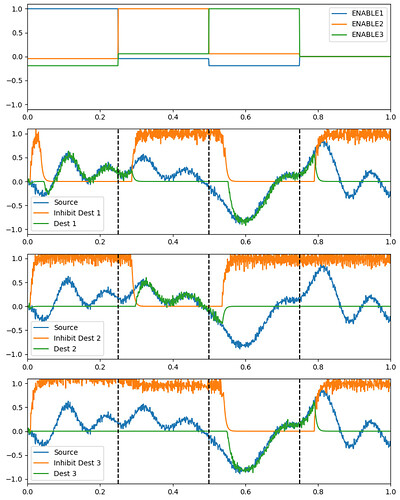
There is activity of the controlled neuron ensemble (i.e. of the speech action ensemble for vowel i → sa_vow_I) already before the syllable oscillator for bi (-> BI_oscillator) is activated. This activation takes place at around 0.6 sec in the simulation, but we can see activation for the vowel bi speech action (magenta) already earlier between 0 sec and 0.6 sec
This artifact does not appear, if I do not include the ensemble modules
connIn_syll2sa_vow_I = EnsembleModule(ens_params={"n_neurons": n_ens_syll2sa, "dimensions": 2})
connOut_syll2sa_vow_I = EnsembleModule(ens_params={"n_neurons": n_ens_syll2sa, "dimensions": 2})
and thus, if I do the direct connection of syllable oscillator for bi and speech action ensemble for vowel i :
nengo.Connection(BI_oscillator.output, sa_vow_I.input, function=CV_signal_sa_vow_I, transform=[vow_vel])
In order to prove that, I as well have attached a second figure which shows the simulation result in case of the direct connection. In this case you see no artifact (no activation of speech action for vowel i before the syllable oscillator becomes active (i.e. see row above in the figure → oscillators).
Do you have any ideas how to solve this problem?
Best
Bernd
In order to give some more details, here the definition for the syllable oscillator (as ensemble module) and for the speech action ensemble module:
# define oscillators for syllables (syll)
n_ens_syll = 2500 # 2500
# Oscillators for each syllable (set intercepts to create a representational deadzone)
BA_oscillator = EnsembleModule(ens_params={"n_neurons": n_ens_syll, "dimensions": 2, "intercepts": Uniform(0.3,1), "encoders": encoders})
DA_oscillator = EnsembleModule(ens_params={"n_neurons": n_ens_syll, "dimensions": 2, "intercepts": Uniform(0.3,1), "encoders": encoders})
GA_oscillator = EnsembleModule(ens_params={"n_neurons": n_ens_syll, "dimensions": 2, "intercepts": Uniform(0.3,1), "encoders": encoders})
PA_oscillator = EnsembleModule(ens_params={"n_neurons": n_ens_syll, "dimensions": 2, "intercepts": Uniform(0.3,1), "encoders": encoders})
TA_oscillator = EnsembleModule(ens_params={"n_neurons": n_ens_syll, "dimensions": 2, "intercepts": Uniform(0.3,1), "encoders": encoders})
KA_oscillator = EnsembleModule(ens_params={"n_neurons": n_ens_syll, "dimensions": 2, "intercepts": Uniform(0.3,1), "encoders": encoders})
MA_oscillator = EnsembleModule(ens_params={"n_neurons": n_ens_syll, "dimensions": 2, "intercepts": Uniform(0.3,1), "encoders": encoders})
NA_oscillator = EnsembleModule(ens_params={"n_neurons": n_ens_syll, "dimensions": 2, "intercepts": Uniform(0.3,1), "encoders": encoders})
LA_oscillator = EnsembleModule(ens_params={"n_neurons": n_ens_syll, "dimensions": 2, "intercepts": Uniform(0.3,1), "encoders": encoders})
# to learn:
BI_oscillator = EnsembleModule(ens_params={"n_neurons": n_ens_syll, "dimensions": 2, "intercepts": Uniform(0.3,1), "encoders": encoders})
DI_oscillator = EnsembleModule(ens_params={"n_neurons": n_ens_syll, "dimensions": 2, "intercepts": Uniform(0.3,1), "encoders": encoders})
GI_oscillator = EnsembleModule(ens_params={"n_neurons": n_ens_syll, "dimensions": 2, "intercepts": Uniform(0.3,1), "encoders": encoders})
PI_oscillator = EnsembleModule(ens_params={"n_neurons": n_ens_syll, "dimensions": 2, "intercepts": Uniform(0.3,1), "encoders": encoders})
TI_oscillator = EnsembleModule(ens_params={"n_neurons": n_ens_syll, "dimensions": 2, "intercepts": Uniform(0.3,1), "encoders": encoders})
KI_oscillator = EnsembleModule(ens_params={"n_neurons": n_ens_syll, "dimensions": 2, "intercepts": Uniform(0.3,1), "encoders": encoders})
MI_oscillator = EnsembleModule(ens_params={"n_neurons": n_ens_syll, "dimensions": 2, "intercepts": Uniform(0.3,1), "encoders": encoders})
NI_oscillator = EnsembleModule(ens_params={"n_neurons": n_ens_syll, "dimensions": 2, "intercepts": Uniform(0.3,1), "encoders": encoders})
LI_oscillator = EnsembleModule(ens_params={"n_neurons": n_ens_syll, "dimensions": 2, "intercepts": Uniform(0.3,1), "encoders": encoders})
and:
n_ens_sa = 2000 # 2000
# Premotor trajectory generators for speech actions "sa"
sa_lab_constr = EnsembleModule(ens_params={"n_neurons": n_ens_sa, "dimensions": 1}) # b, p, m,
sa_api_constr = EnsembleModule(ens_params={"n_neurons": n_ens_sa, "dimensions": 1}) # d, t, n,
sa_dor_constr = EnsembleModule(ens_params={"n_neurons": n_ens_sa, "dimensions": 1}) # g, k, N,
sa_lat_constr = EnsembleModule(ens_params={"n_neurons": n_ens_sa, "dimensions": 1}) # lateral
sa_vel_abduc = EnsembleModule(ens_params={"n_neurons": n_ens_sa, "dimensions": 1}) # nasal
sa_glott_abduc = EnsembleModule(ens_params={"n_neurons": n_ens_sa, "dimensions": 1}) # voiceless sounds
sa_vow_I = EnsembleModule(ens_params={"n_neurons": n_ens_sa, "dimensions": 1}) # vowel I ii
sa_vow_A = EnsembleModule(ens_params={"n_neurons": n_ens_sa, "dimensions": 1}) # vowel A aa
sa_vow_U = EnsembleModule(ens_params={"n_neurons": n_ens_sa, "dimensions": 1}) # vowel U uu
sa_final = EnsembleModule(ens_params={"n_neurons": n_ens_sa, "dimensions": 1}) # end of syllable -> feedback signal
Kind regards
Bernd
www.speechtrainer.eu
Hi @bernd,
I looked over your problem description and code and from what I understand, the what your are trying to accomplish is to do this:
BI_oscillator >> sa_vow_I
but have the connection be controlled by the BG rules, correct?
Now, the issue you are having is that connections made by the BG rules cannot have functions attached to them (at least, not functions in the standard Nengo sense).
It looks like you attempted to circumvent this problem by creating two EnsembleModule objects, and using the BG to control the flow of information between the two. This solution is definitely a valid solution, and from what I can tell, it should work.
Looking at your code, it seems like you may have made a mistake in the second connection. It currently reads:
nengo.Connection(connIn_syll2sa_vow_I.output, sa_vow_I.input, function=CV_signal_sa_vow_I, transform=[vow_vel])
whereas, I believe it should read (changed connIn_syll2sa_vow_I to connOut_syll2sa_vow_I):
nengo.Connection(connOut_syll2sa_vow_I.output, sa_vow_I.input, function=CV_signal_sa_vow_I, transform=[vow_vel])
Making the above change should address the artifacts that you are observing in your output.
With regards to debugging such complex systems, sometimes, it is helpful to plot just the necessary plots needed to narrow down the issue. For the artifact you are seeing, since it was isolated to the SPA connection, plotting the outputs of the components involved in that connection (i.e., BI_oscillator.output, connIn_syll2sa_vow_I.output, connOut_syll2sa_vow_I.output, sa_vow_I.input) would help illuminate the cause of the issue.
Additionally, if you could convert the BI_oscillator network / ensemble into an SPA module (maybe call it OscillatorModule and use the EnsembleModule as a template, you should be able to remove one of the intermediary EnsembleModules which will reduce the delays caused by the multiple synaptic connections between BI_oscillator and sa_vow_I.
As an example, if you convert BI_oscillator into an SPA module, you should be able to do this:
conn_syll2sa_vow_I = EnsembleModule(ens_params={"n_neurons": n_ens_syll2sa, "dimensions": 2})
BI_oscillator >> conn_syll2sa_vow_I # You can put this in the BG-THAL rules later
nengo.Connection(conn_syll2sa_vow_I.output, sa_vow_I.input, function=CV_signal_sa_vow_I, transform=[vow_vel])
Dear Xuan
thank you for looking in depth in my problem. Yes, the “mistake” is just a shortening up of the code: I wanted to see how it works, if I just use one intermediate buffer
connIn_syll2sa_vow_I
between the both SPA-module ensembles:
BI_oscillator and sa_vow_I
If I “correct” that by introducing two intermediate buffers
connIn_syll2sa_vow_I and connOut_syll2sa_vow_I
the problem with the artifact stays.
You are right: I have to plot the activity of more buffers like the connIn and connOut buffers in order to see what is going on in detail. I will do that and think about my problem a little longer before writing you again.
Thanks so far
Bernd
I should point out that another debugging step would be to isolate where the errant signal is coming from. Once you have applied probes to the intermediate ensembles, you can break the chain (i.e., do not connect connOut_syll2sa_vow_I to sa_vow_I), and see if the artifact still shows up at the connOut_syll2sa_vow_I output.
If it does, I suspect that because sa_vow_I is an oscillator, noise from the connOut_syll2sa_vow_I ensemble may be causing a premature activation of the oscillator. You can address this issue by introducing a “dead zone” into the ensemble. Basically, you adjust the ensemble’s intercepts so that below a certain threshold, the ensemble is completely quiet (no spikes at all). This will impact the representational power of the ensemble (because you are introducing a discontinuity in the response curve, and because the response curves no longer span the entire range of inputs), so more neurons may be needed in those intermediate ensembles. You can adjust the ensemble intercepts like so:
ens = nengo.Ensemble(..., ..., intercepts=nengo.dists.Uniform(0.1, 1))
The code above, for example, will make it so that any inputs < 0.1 in vector magnitude will result in the ensemble not spiking.
Dear Xuan
this solution seems to work. But I still need to check it with more than just one example.
Thank you for that idea
Best
Bernd
Dear Xuan
I have a further question concerning my syllable oscillators: like BA_oscillator
# define oscillators for syllables (syll)
n_ens_syll = 2500 # 2500
# Oscillators for each syllable (set intercepts to create a representational deadzone)
BA_oscillator = EnsembleModule(ens_params={"n_neurons": n_ens_syll, "dimensions": 2, "intercepts": Uniform(0.3,1), "encoders": encoders})
which includes the typical recursive connection for becoming an oscillator:
# Set recurrent connections on oscillators with parameters for adjusting oscillation frequency.
tau = 0.025 # Adjust to avoid multiple oscillations.
# needs to be adjusted together with freq, if freq. is above 2.0 Hz!
freq = 1 # 2.0
omega = tau*2*np.pi*freq
nengo.Connection(BA_oscillator.output, BA_oscillator.input, transform=[[1, -omega], [omega, 1]], function=zone, synapse=tau)
and which is triggered by an S-pointer from a state buffer: (start of the syllable)
here shown for different syllables:
# Set input connections on oscillators
nengo.Connection(model.motor_syll_init_ok.selection.output[0], MA_oscillator.input, transform=[[-1],[0]]) # ma
nengo.Connection(model.motor_syll_init_ok.selection.output[1], PA_oscillator.input, transform=[[-1],[0]]) # pa
nengo.Connection(model.motor_syll_init_ok.selection.output[2], TA_oscillator.input, transform=[[-1],[0]]) # ta
nengo.Connection(model.motor_syll_init_ok.selection.output[8], LA_oscillator.input, transform=[[-1],[0]]) # la
nengo.Connection(model.motor_syll_init_ok.selection.output[14], BA_oscillator.input, transform=[[-1],[0]]) # ba
My question now is:
Because the speech sounds appearing within each syllable are triggered by syllable phase values appearing as points in time if the BA_oscillator is running, each syllable is represented by exactly one oscillation cycle.
In order to guarantee this, we introduce a specific “dead zone” function. Thus, only one oscillation cycle is performed:
# Define encoders and a function for building oscillators that perform a single oscillation once triggered.
f1 = 7.5/8.0
encoders = [[np.cos(theta), np.sin(theta)] for theta in np.random.uniform(-np.pi, f1*np.pi, 2500)]
def zone(x):
theta = math.atan2(x[1], x[0])
if theta > f1*np.pi:
return 0
else:
return x
Because I did not develop this solution by myself, my question is:
What exactly is the motivation for using exactly this function for defining the syllable oscillator encoders ?
(Terry gave me this solution years ago but I never understood this solution in detail and now I can not reach Terry anymore easily)
Thank you for helping me with this problem
Best
Bernd
P.S.: In addition I attach a figure showing the phase diagram of a syllable oscillator which (i) ends after exactly one period (above: syllable TAP) and reactivated much later and (ii) a syllable oscillator which already is activated a second time right during its first oscillator cycle because the syllable is repeated earlier or faster
Hey @bernd,
Looking at the behaviour of the oscillator in your plots, it looks like what Terry was trying to accomplish with his code is to have the oscillator start, then stop just before a full cycle of the oscillator has been reached. Two parts of his code is needed to make this happen:
zone functionintercepts
I made a test script to experiment with a very basic oscillator based on Terry’s code. You can play with it here: test_osc.py (1.6 KB)
The first thing I will discuss is the zone function. If you look at the zone function, what it is doing is returning a value of x when \theta <= f1 * \pi, and returning a value of 0 when \theta > f1 * \pi. Since f1 is 7.5/8.0, what this is doing is saying that the oscillator should operate normally for about 94% of the full cycle, and in the last 6% of the cycle, the feedback of the oscillator should try to go to 0.
If you run my test script with:
use_encoders = False
use_intercepts = False
use_zone = True
this will only use the zone function and nothing else in the test network. If you do so, you will get a plot like so:
From the plot we can see that the zone function does a pretty good job of trying to make the oscillator only do 1 cycle. The oscillator starts, goes almost a full circle, and just before the end, the output shrinks close to 0. However, with just the zone function, we see that even after being commanded to stop, the oscillator doesn’t fully do so, but instead just ends up oscillating in a smaller radius. To improve the stopping behaviour, we need to use the intercepts.
One cool thing you can do with ensembles is to change the intercepts to accomplish non-linear functions. If you look at this Nengo example, it plays around with intercepts to achieve a “sharper” non-linearity for a step function. However, for Terry’s code, the intercepts are being used to create a “dead zone” in the ensemble’s representational range.
I created a 1D version of an ensemble with the intercepts here that you can play with:
test_intercepts.py (891 Bytes)
The ensemble has an input that linearly increases from -1 to 1 over 2 seconds. If you use the standard Nengo intercepts, you will see that the output of the ensemble is just a normal communication channel. However, if you use the custom intercepts, you will observe that the output of the ensemble falls to 0 when the input is between -0.3 and 0.3. Thus, a “dead zone” (no output spikes are generated) in this range of values.
Now, what happens if we combine the custom intercepts with the oscillator network? When you project the 2D ensemble into 1-dimension, the vector magnitude of the oscillators current position becomes the x input to the 1D ensemble. So, if you create an ensemble with an intercept of (0.3, 1), any vector representation with a magnitude < 0.3 will result in no output from the oscillator.
If you look at the previous oscillator output (the one with just the zone function), you see that for most of the cycle, the vector magnitude of the oscillator output is roughly 1. Nearing the end, the zone function pushes the output of the oscillator closer to (0,0), so the vector magnitude of the oscillator output gradually decreases. If we combine the zone function with the (0.3, 1) intercept values, when the zone function pushes the magnitude of the oscillator output to < 0.3, it will go into this “dead zone” and stop producing any output, thus stopping the oscillator from cycling (or rather, the oscillator will cycle at a radius of 0). If you run my test_osc.py with:
use_encoders = False
use_intercepts = True
use_zone = True
you will see something like this:
Which accomplishes our goal of having the oscillator do 1 cycle and then stop.
The one thing I can’t figure out is what the custom encoders do… From my understanding of the oscillator (and from those I have built myself), these custom encoders are not really necessary. The one reason I can see for the encoders is that since the oscillator should have no output when the zone function is trying to force the output to 0, Terry has configured the encoder distribution to maximize the encoders to be within the “useful” range of values. But, if you run my test code with and without the custom encoders, the output doesn’t seem to change very much, so I leave it up to you to decide whether or not to include it in your model. It might be that the encoders have some other effect that is not apparent in my simple test model.
Dear Xuan
thank you very much for your detailed answer.
That helped me a lot:
1 ) The non-default definition for the “encoders” was always strange for me and I will replace it by using standard encoding in my code from now on.
2 ) Yes, I was always thinking that only the recurrent connection does the main work: (as is exemplified by your great py-example):
So: this is important:
nengo.Connection(
osc, osc, transform=[[1, -omega], [omega, 1]], function=zone, synapse=tau
)
And in addition it is now clear for me that the zone function defines the return of the oscillation after one cycle.
3 ) In addition the non-default intercepts definition allows the clear reaching of the 0,0 point in the phase space.
Great to have this knowledge now!
I now understand a little more about basic definition of attributes for ensembles and connections
Thank you again
Kind regards
Bernd