Since backpropagation can’t be used to train a network with LIF neurons, which other algorithms are there to do something like what backprop does? I’m not talking about an algorithm with which we can achieve state of the art results, but I want to know what other alternative algorithms are there and if someone has tried to experiment with them.
Here’s a great review paper on the whole area:
There are a number of ideas on how a biological system might implement supervised deep learning. Here are a few papers looking into the topic, though in my opinion, only the first really proposes something that a biological system could implement:
https://www.nature.com/articles/ncomms13276
I’m looking into this as part of my thesis, so I’ll let you know when I have something ready to read 
Thanks a lot for the links! I’ve been reading a bit of target-prop, but the algorithm that the first link mentions is completely new for me, is the first time I read about feedback alignment.
Perhaps, this might help…
Gradient Descent for Spiking Neural Networks! Came out just a few days ago and is still under review, I think.
I’ve been reading a little bit about Feedback Alignment Algotithms and found your work @Eric http://compneuro.uwaterloo.ca/publications/hunsberger2017a.html#hunsberger2017acite
Please tells us when your are releasing some papers and implementation examples, it will be awesome to see them
I am doing something similar, using thiese kind of learning rules in a RL setting for my master thesis. A good explanation is from Baldi et al. [1612.02734] Learning in the Machine: Random Backpropagation and the Deep Learning Channel . Actually I was wondering @Eric, considering that you did some work on this, if PES has a correlation to skipped random backpropagation as mentioned in the paper from Baldi? I am sure you have read it in the process. It seems similar since the correction in PES is encoded, the encoders could be seen as analogous to post-synaptic random weight matrices in srbp.
Hi @trix. There’s definitely some strong similarities between PES and skipped random backpropagation (SRBP), and they might actually be closer than I originally thought.
In the case of PES, you have something like this:
![]()
where Wij is the weight from presynaptic neuron i to postsynaptic neuron j, ai is the activity of neuron i, and Ekj is the random encoder from input k to neuron j, which we use to map the error ek into the neuron space.
In the case of SRBP, you have:
![]()
which is the same as above, except we have the derivative of the postsynaptic neuron at the current activation level a’j as a third term. (Here, Bkj is the random backwards projection, which as you pointed out, functions almost identically to random encoders.)
So really the only difference is the inclusion of this derivative term in the case of SRBP. I’ve found that it is important for the stability of the algorithm to have this; with no derivative, much smaller learning rates are needed to maintain stability, which hampers learning, and even then I don’t think stability is guaranteed (though I’m not sure if it’s ever guaranteed with RBP).
The other difference is the way in which these learning rules tend to be used. I’m not sure if anyone has used PES for deep networks before, whereas that’s the whole point of SRBP. This is what makes your observation so insightful, since it draws a connection between two things that I had previously thought of as separate. PES also has strong theoretical motivations; we use the random encoders in the learning rule because they allow us to map the error from the state space of the population to the neuron space. That is, in a classification problem, we think of our postsynaptic population as “representing” the class of the stimulus, and the encoders as being the mapping from a one-hot representation of the class to the neuron activities. This is the key to the derivation of the PES rule.
When we have multiple layers, this theoretical connection begins to break down, which is why I think no one has thought to use PES in a multi-layer situation as one would SRBP. It makes sense to think of the final layer as representing the stimulus class, but could this intuition apply to earlier layers, too? I’m not sure what exactly that would entail, but it seems interesting to think about.
I hope that makes sense, and I’m interested in hearing more of your thoughts on this. I’m still trying to figure out what this possible connection means for both PES and SRBP. Thanks for pointing it out!
Thanks for the elaborate reply @Eric
Actually in the paper from Baldi raw SRBP doesn’t necessarily include the postsynaptic derivative, although yes, it makes sense that including the derivative makes it more stable, which can be seen from the results in the paper where versions without the derivative had decaying performance over time. I would expect the same thing from PES in a 4 layer setting.
My understanding is that the presynaptic activity alone doesn’t state anything about the contribution to the output, since the postsynaptic neuron doesn’t necessarily spike given some presynaptic activity. Probably adding the activity of the post-neuron to the equation and making it
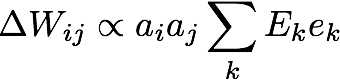
in which case the rule becomes Hebbian, would make it more stable and perhaps trainable for multiple layers. What would make even more sense is to take some kind of derivative approximate with regards to the voltage of the post-synaptic neuron in the case of SNNs, something similar was already done by approximating the derivative of the transfer function by a boxcar function of the postsynaptic current in the case of a current-based model, which allowed multi-layer spike based training, dubbed event-driven backpropagation.
I guess you are doing something similar with the upcoming paper on RBP in SNNs, although you are genuinely doing RBP and not SRBP and therefore back-propagating the error with feedback weights as I understood? I am interested in how you solved the transfer function derivative for the LIF.
Then I would say that in the case without the postsynaptic transfer function derivative that SRBP is in fact equivalent to PES.